2022-2023学年江苏省常州市金坛区华罗庚中学高一（上）期中数学试卷

一、单选题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项符合题目要求.

• 1．已知A={-2，0，2}，B={-3，-2，2}，则A∪B的真子集的个数为（　　）

  A．3

  B．7

  C．15

  D．31
  组卷：5引用：2难度：0.8

  解析

• 2．等式|a+b|=|a|+|b|成立的充要条件是（　　）

  A．ab=0

  B．ab＜0

  C．ab≥0

  D．ab≤0
  组卷：139引用：6难度：0.8

  解析

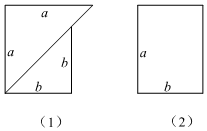• 3．如图两种广告牌，其中图（1）是由两个等腰直角三角形构成的，图（2）是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种关系用含字母a,b（a≠b）的不等式表示出来（　　）

  A． 1 2 （ a 2 + b 2 ） ＞ ab	B． 1 2 （ a 2 + b 2 ） ＜ ab
  C． 1 2 （ a 2 + b 2 ） ≥ ab	D． 1 2 （ a 2 + b 2 ） ≤ ab
  组卷：86引用：3难度：0.7

  解析

• 4．已知函数f（x）的定义域为（-1，1），函数g（x）=f（2x-1），则函数g（x）的定义域为（　　）

  A．（-1，1）	B．（0，1）
  C．（-3，1）	D．（f（-3），f（1））
  组卷：360引用：3难度：0.9

  解析

• 5．今有2个红球、3个黄球、4个白球，同色球不加以区分，将这9个球排成一列的排法总数为（　　）

  A．1782

  B．1720

  C．2520

  D．1260
  组卷：89引用：2难度：0.7

  解析

• 6．若关于x的不等式|x-1|+|x-2|≤a²+a+1（a∈R）的解集为空集，则实数a的取值范围是（　　）

  A．-1＜a＜0

  B．0＜a＜1

  C．1＜a＜2

  D．a＜-1
  组卷：189引用：3难度：0.7

  解析

• 7．偶函数f（x）的定义域为R，且对于任意x₁，x₂∈（-∞，0]（x₁≠x₂），均有

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ＜0成立，若f（1-a）＜f（2a-1），则实数a的取值范围为（　　）

  A． （ 2 3 ， + ∞ ）	B． （ - ∞ ， 0 ） ∪ （ 2 3 ， + ∞ ）
  C． （ 0 ， 2 3 ）	D． （ 0 ， 2 3 ]
  组卷：64引用：2难度：0.6

  解析

四、解答题（本大题共6小题，共70分）

• 21．已知函数f（x）=-x|x-2a|+1（x∈R）．
  （1）当a=1时，求函数y=f（x）的零点；
  （2）当a∈

  （

  0

  ，

  3

  2

  ）

  ，求函数y=f（x）在x∈[1，2]上的最大值．
  组卷：371引用：2难度：0.1

  解析

• 22．若函数y=f（x）自变量的取值区间为[a,b]时，函数值的取值区间恰为

  [

  2

  b

  ，

  2

  a

  ]

  ，就称区间[a,b]为y=f（x）的一个“和谐区间”．已知函数g（x）是定义在R上的奇函数，当x∈（0，+∞）时，g（x）=-x+3．
  （1）求g（x）的解析式；
  （2）求函数g（x）在（0，+∞）内的“和谐区间”；
  （3）若以函数g（x）在定义域内所有“和谐区间”上的图象作为函数y=h（x）的图象，是否存在实数m,使集合{（x,y）|y=h（x）}∩{（x,y）|y=x²+m}恰含有2个元素．若存在，求出实数m的取值集合；若不存在，说明理由．
  组卷：434引用：14难度：0.4

  解析