2023-2024学年天津四十七中高二（上）第一次月考数学试卷（10月份）

一、选择题：（在每小题给出的四个选项中，只有一项是符合题目要求的.本大题共9个小题，每题5分，共45分.）

• 1．直线x+

  3

  y-8

  3

  =0的倾斜角为（　　）

  A． π 6

  B． π 4

  C． 2 π 3

  D． 5 π 6
  组卷：242引用：7难度：0.8

  解析

• 2．“a=-3”是直线l₁：ax+（1-a）y=3与l₂：（a-1）x+（2a+3）y=2互相垂直的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：94引用：1难度：0.5

  解析

• 3．设x,y∈R，向量

  a

  =（x,1，1），

  b

  =（1，y,1），

  c

  =（2，-4，2），且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，则|2

  a

  +

  b

  |=（　　）

  A．2 2

  B．3 2

  C．3

  D． 10
  组卷：282引用：11难度：0.8

  解析

• 4．圆x²-4x+y²=0与圆x²+y²+4x+3=0的公切线共有（　　）

  A．1条

  B．2条

  C．3条

  D．4条
  组卷：781引用：9难度：0.8

  解析

• 5．已知M是圆C：x²+y²=1上的动点，点N（2，0），则MN的中点P的轨迹方程是（　　）

  A．（x-1）2+y2= 1 4	B．（x-1）2+y2= 1 2
  C．（x+1）2+y2= 1 2	D．D、（x+1）2+y2= 1 4
  组卷：118引用：4难度：0.9

  解析

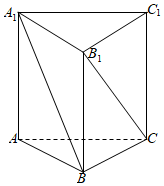• 6．如图，已知正三棱柱ABC-A₁B₁C₁的棱长均为2，则异面直线A₁B与B₁C角的余弦值是（　　）

  A． 3 2

  B． 1 2

  C． 1 4

  D．0
  组卷：572引用：16难度：0.7

  解析

三、解答题.（本大题共5小题，共75分）解答应写出文字说明，证明过程或演算步骤.

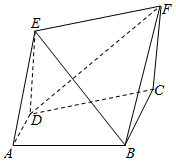• 19．如图所示，直角梯形ABCD中，AD∥BC，AD⊥AB，AB=BC=2AD=2，四边形EDCF为矩形，CF=

  3

  ，平面EDCF⊥平面ABCD．
  （Ⅰ）求证：DF∥平面ABE；
  （Ⅱ）求平面ABE与平面EFB所成锐二面角的余弦值．
  （Ⅲ）在线段DF上是否存在点P，使得直线BP与平面ABE所成角的正弦值为

  3

  4

  ？若存在，求出线段BP的长，若不存在，请说明理由．
  组卷：3218引用：18难度：0.1

  解析

• 20．已知圆M与直线3x-

  7

  y+4=0相切于点

  （

  1

  ，

  7

  ）

  ，圆心M在x轴上．
  （1）求圆M的标准方程；
  （2）若直线l：（2m+1）x+（m+1）y=7m+4（m∈R）与圆M交于P，Q两点，求弦PQ的最短长度．
  （3）过点M且不与x轴重合的直线与圆M相交于A，B两点，O为坐标原点，直线OA，OB分别与直线x=8相交于C，D两点，记△OAB，△OCD的面积为S₁，S₂，求

  S

  1

  S

  2

  的最大值．
  组卷：242引用：8难度：0.5

  解析