2022-2023学年黑龙江省哈尔滨四十九中学年九年级（上）质检数学试卷（12月份）（五四学制）

一、选择题（每题3分，共计30分）

• 1．下列图案中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：24引用：2难度：0.9

  解析

• 2．已知抛物线的解析式为y=-（x+3）²+2，则这条抛物线的顶点坐标是（　　）

  A．（2，3）

  B．（3，2）

  C．（-3，2）

  D．（2，2）
  组卷：38引用：1难度：0.6

  解析

• 3．若反比例函数y=

  m

  +

  3

  x

  的图象在第二、四象限，则m的取值范围是（　　）

  A．m＞0

  B．m＜0

  C．m＞-3

  D．m＜-3
  组卷：1320引用：8难度：0.8

  解析

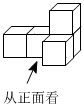• 4．如图是用5个相同的立方体搭成的几何体，其俯视图是（　　）

  A．

  B．

  C．

  D．
  组卷：117引用：5难度：0.7

  解析

• 5．将抛物线y=x²-1向左平移2个单位长度，再向上平移2个单位长度，所得抛物线的解析式为（　　）

  A．y=（x+3）2+2

  B．y=（x+2）2+2

  C．y=（x+2）2+1

  D．y=（x-2）2+2
  组卷：714引用：9难度：0.6

  解析

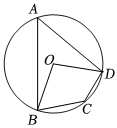• 6．如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DCB等于（　　）

  A．90°

  B．100°

  C．130°

  D．140°
  组卷：196引用：3难度：0.7

  解析

• 7．如图，一把梯子AB靠在垂直水平地面的墙上，梯子底端A到墙面的距离AC为6米，若梯子与地面的夹角为α，则梯子AB的长为（　　）

  A．6sinα米

  B．6cosα米

  C． 6 sinα 米

  D． 6 cosα 米
  组卷：313引用：3难度：0.6

  解析

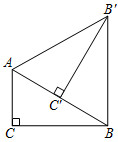• 8．如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C'，使点C'落在AB边上，连接BB'，则BB'的长度是（　　）

  A．1cm

  B．2cm

  C． 3 cm

  D．2 3 cm
  组卷：3603引用：44难度：0.5

  解析

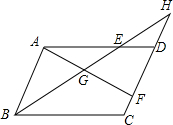• 9．如图，在▱ABCD中，E、F分别是AD、CD边上的点，连接BE、AF，它们相交于点G，延长BE交CD的延长线于点H，下列结论错误的是（　　）

  A． AE ED = BE EH

  B． EH EB = DH CD

  C． EG BG = AE BC

  D． AG FG = BG GH
  组卷：247引用：13难度：0.7

  解析

三、解答题（21～22题各7分，2324题各8分，25～27题各10分，共计60分）

• 26．已知，AB为⊙O的直径，弦AC、DE交于点F，连接OF，DF=AF．
  （1）如图1，求证：∠CFO=∠EFO；
  （2）如图2，连接BE，若∠ABE+2∠FOA=90°，求证：FA=FO；
  （3）如图3，在（2）的条件下，连接FO并延长交BE于点Q，若CF-AF=8，EQ：BQ=13：5，求OB的长．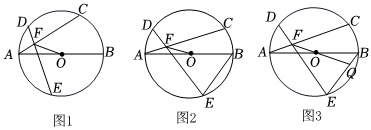
  
  组卷：63引用：1难度：0.1

  解析

• 27．在平面直角坐标系中，点O为坐标原点，抛物线y=ax²+bx-4与x轴交于点A、B，与y轴交于点C，直线y=x-4经过B、C两点，OB=4OA．
  （1）如图1，求抛物线解析式；
  （2）如图2，点P为第一象限抛物线上一点，过点P作PD⊥x轴交BC于点D，交AB于点E，设点P的横坐标为t,线段PD的长为d,求d与t的函数关系式（不要求写出自变量t的取值范围）；
  （3）如图3，在（2）的条件下，当d=4时，点M是直线PD上一点，BN∥PM，连接MN，过点A作AH⊥MN垂足为H，延长AH交BN于点F，交抛物线于点Q，当∠HFN=2∠HMF，MN+NF=5时，求点Q的坐标．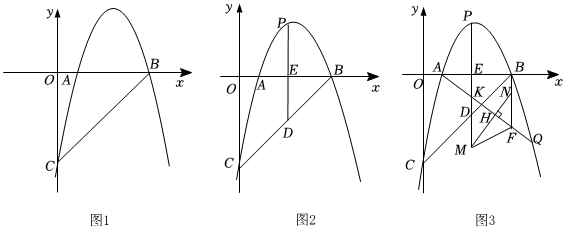
  
  组卷：130引用：1难度：0.1

  解析