当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省永州市冷水滩区李达中学九年级（上）入学数学试卷

发布：2024/7/31 8:0:9

一、选择题（本大题共12个小题，每小题3分，共36分）

1．中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（　　）
A． B． C． D．
组卷：1274引用：58难度：0.8
解析
2．在平面直角坐标系中，点M（-2，1）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：1445引用：95难度：0.9
解析
3．一个多边形的内角和是外角和的2倍，这个多边形的边数为（　　）
A．5 B．6 C．7 D．8
组卷：3972引用：124难度：0.9
解析
4．下列各组数中，是勾股数的是（　　）
A．8，24，25 B．8，15，17 C．10，20，26 D．14，36，39
组卷：242引用：7难度：0.5
解析
5．下列函数中，是正比例函数的是（　　）
A．y=2x-1 B．
y
=
1
x
+
1
C．
y
=
x
2
D．y=2x²+1
组卷：277引用：2难度：0.5
解析
6．下列说法正确的是（　　）
A．平行四边形既是轴对称图形又是中心对称图形
B．三个角是直角的四边形是矩形
C．菱形的对角线相等且互相平分
D．对角线垂直平分的四边形是正方形
组卷：36引用：1难度：0.7
解析
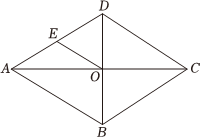7．如图，菱形ABCD的对角线AC，BD交于点O，点E为边AD的中点，若AC=8cm,BD=6cm,则线段OE的长度是（　　）
A．4cm B．3cm C．2.5cm D．2cm
组卷：469引用：5难度：0.8
解析
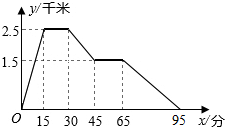8．图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中x表示时间，y表示张强离家的距离．根据图象提供的信息，以下四个说法错误的是（　　）
A．体育场离张强家2.5千米
B．体育场离早餐店4千米
C．张强在体育场锻炼了15分钟
D．张强从早餐店回家的平均速度是3千米/小时
组卷：162引用：7难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共8个小题，共66分）

25．某数学学习小组在学习《勾股定理》之后进行了拓展研究，类比勾股定理，新定义一种三角形，规定：如果一个三角形两边的平方和等于第三边平方的2倍，那么称这个三角形为“奇异勾股三角形”，请根据“奇异勾股三角形”的定义，完成下列问题：
（1）判断：下列说法正确的是
（填甲、乙、丙）
组员甲说：等边三角形一定是“奇异勾股三角形”；
组员乙说：等腰直角三角形也是“奇异勾股三角形”；
组员丙说：三边长分别为
2
，2，
6
的三角形也是“奇异勾股三角形”．
（2）若△ABC是“奇异勾股三角形”．且两边长分别为1，
7
，求第三边的长；
（3）若Rt△ABC是“奇异勾股三角形”，且三边长分别为a,b,c（a,b为直角边，c为斜边，且a＜b）．求Rt△ABC的周长（用只含有a的式子表示）．
组卷：169引用：4难度：0.6
解析
26．如图1，在边长为1的正方形ABCD中，AE平分∠BAC，交BC于点E，过点E作EF⊥AC于点F，延长FE交AB的延长线于点H，过点F作FG∥BC交AE于点G，连接BG．
（1）求证：BH=FC；
（2）求证：四边形BEFG是菱形；
（3）如图2，点M是CD的中点，点P是AD上的动点，点N是对角线AC上的动点，请问PM+PN是否有最小值？如果有，求出最小值；如果没有，请说明理由．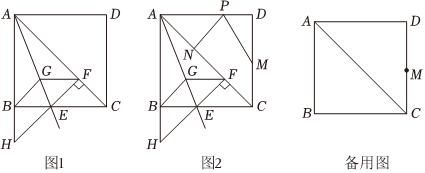
组卷：153引用：4难度：0.4
解析