2022-2023学年广东省广州市花都区八年级(下)期末数学试卷
发布:2024/6/29 8:0:10
一、选择题。(本大题共10题,每题3分,满分30分.在每题给出的四个选项中,只有一项是符合题目的要求.)
-
1.下列根式是最简二次根式的是( )
组卷:218引用:3难度:0.8 -
2.校运会100米短跑项目预赛中,15名运动员的成绩各不相同,取前8名参加决赛,其中运动员小军已经知道自己的成绩,他想确定自己是否进入决赛,需要知道这15名运动员成绩的( )
组卷:292引用:4难度:0.7 -
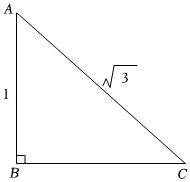 3.根据如图所示的数据,BC的长为( )组卷:179引用:3难度:0.7
3.根据如图所示的数据,BC的长为( )组卷:179引用:3难度:0.7 -
4.下列函数中,是一次函数的是( )
组卷:369引用:3难度:0.5 -
5.下列二次根式的运算正确的是( )
组卷:248引用:4难度:0.5 -
 6.如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,则△OCD的周长为( )
6.如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,则△OCD的周长为( )
组卷:275引用:1难度:0.5 -
7.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,则该沙田的面积为( )平方里.
组卷:147引用:4难度:0.9 -
8.对于一次函数y=-2x+4,下列结论正确的是( )
组卷:833引用:6难度:0.7
三、解答题。(本大题共9题,满分72分.解答须写出文字说明、证明过程和演算步骤.)
-
24.如图,在梯形ABCD中,∠A=90°,AD∥BC,AD=20cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒.问:
(1)AP边的长度为 cm,PD边的长度为 cm,(用t的式子表示),其中t的取值范围为 ;
(2)当t为何值时,四边形PBQD是平行四边形,请说明理由;
(3)朱华同学研究发现:按以上变化,四边形PBQD在变化过程中不可能为菱形,除非改变动点的运动速度.请探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求此时点Q的速度.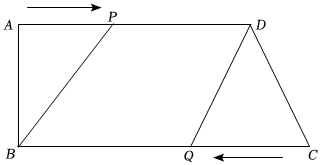 组卷:456引用:1难度:0.2
组卷:456引用:1难度:0.2 -
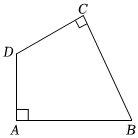 25.定义:如图,只有一组对角是直角的四边形叫做“损矩形”.
25.定义:如图,只有一组对角是直角的四边形叫做“损矩形”.
(1)如图1,点P在直线y=x上且横坐标是4,点E(0,2),点F(6,0),连接PE,PF;
判断:四边形PEOF 损矩形(填“是”或“不是”);
(2)如图2,点E在y轴正半轴上,点F在x轴正半轴上,点P是直线y=x上位于第一象限的一个动点,四边形PEOF是“损矩形”,请确定:OE+OF与OP的数量关系,并说明理由;
(3)如图3,若M(0,6),N(8,0),
①在直线l2:y=2x上找一个点Q,使得四边形QMON为损矩形,求点Q的坐标;
②在①的条件上,若K点也在直线l2:y=2x(x>0)上且S△KMN=s四边形QMON,请直接写出K的坐标.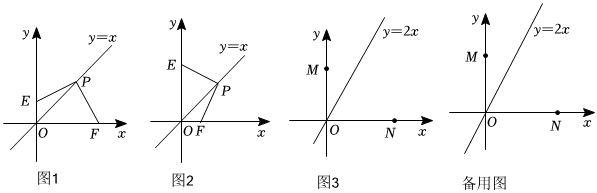 组卷:659引用:2难度:0.2
组卷:659引用:2难度:0.2


