2023-2024学年福建省泉州一中八年级（上）第一次月考数学试卷

一、选择题（共10小题，共40分）

• 1．下列实数中属于无理数的是（　　）

  A．3.14

  B．-2

  C． 2

  D． 1 3
  组卷：54引用：4难度：0.8

  解析

• 2．下列计算正确的是（　　）

  A．（a2）3=a6

  B．a6÷a2=a3

  C．a3•a4=a12

  D．a2-a=a
  组卷：746引用：17难度：0.8

  解析

• 3．下列算式中，正确的是（　　）

  A． 25 =±5

  B．± 9 =3

  C． （ - 2 ） 2 =-2

  D． 3 - 1 =-1
  组卷：832引用：12难度：0.9

  解析

• 4．已知一个正数的两个平方根分别为3a-5和7-a,则这个正数的立方根是（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：1421引用：13难度：0.9

  解析

• 5．已知3^m=4，3^2m-4n=2．若9ⁿ=x,则x的值为（　　）

  A．8

  B．4

  C．2 2

  D． 2
  组卷：1217引用：11难度：0.9

  解析

• 6．下列条件能判定△ABC≌△DEF的一组是（　　）

  A．∠A=∠D，∠B=∠E，∠C=∠F

  B．AB=DE，BC=EF，∠A=∠D

  C．∠A=∠D，∠C=∠F，AC=DF

  D．△ABC的周长等于△DEF的周长
  组卷：1618引用：14难度：0.6

  解析

• 7．利用乘法公式判断，下列等式何者成立？（　　）

  A．2482+248×52+522=3002

  B．2482-248×48-482=2002

  C．2482+2×248×52+522=3002

  D．2482-2×248×48-482=2002
  组卷：734引用：9难度：0.7

  解析

• 8．如果（x²+px+q）（x²-5x+7）的展开式中不含x²与x³项，那么p与q的值是（　　）

  A．p=5，q=18

  B．p=-5，q=18

  C．p=-5，q=-18

  D．p=5，q=-18
  组卷：6394引用：18难度：0.5

  解析

三、解答题

• 24．已知a,b都是正数，ab为定值，求证：当a=b时，a+b有最小值2

  ab

  ．
  证明：∵a＞0，b＞0，
  ∴（

  a

  -

  b

  ）²≥0，
  ∴a+b-2

  ab

  ≥0，即a+b≥2

  ab

  ，
  ∴当a=b时，有（

  a

  -

  b

  ）²=0，
  ∴a+b=2

  ab

  ，即a+b有最小值2

  ab

  ．
  请利用上述结论，解答下列问题：
  （1）若a＞0，则当a=

  时，a+

  4

  a

  取得最

  值，为

  ；
  （2）若a＞1，求代数式a+

  25

  a

  -

  1

  的最小值；
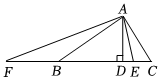
  （3）如图，在△ABC中，∠BAC=90°，AB=a,AC=b,点E在BC上，且BE=AB，点F在CB延长线上，且BF=AC．已知△ABC的面积为

  9

  2

  ，求线段EF的最小值．
  组卷：103引用：1难度：0.5

  解析

• 25．如图1，△ACB为等腰三角形，∠ABC=90°，点P在射线BC上（不与点B，点C重合），以AP为腰长作等腰Rt△PAQ，QE⊥AB于点E．
  
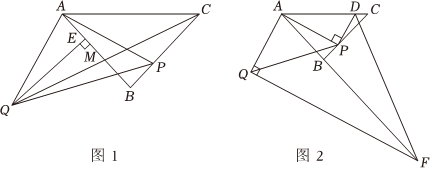
  （1）当点P在线段BC上（不与点B，点C重合），求证：△PAB≌△AQE；
  （2）在（1）的条件下，连接CQ交AB于点M，若PC=2PB，求

  PC

  MB

  的值；
  （3）如图2，过点Q作QF⊥AQ于直线AB于点F，过点P作DP⊥AP交直线AC于点D，连接DF．则点P在运动过程中，线段DF、QF与DP有怎样的数量关系？请说明理由．
  组卷：198引用：2难度：0.5

  解析