已知a,b都是正数，ab为定值，求证：当a=b时，a+b有最小值2

ab

．
证明：∵a＞0，b＞0，
∴（

a

-

b

）²≥0，
∴a+b-2

ab

≥0，即a+b≥2

ab

，
∴当a=b时，有（

a

-

b

）²=0，
∴a+b=2

ab

，即a+b有最小值2

ab

．
请利用上述结论，解答下列问题：
（1）若a＞0，则当a=

2

2

时，a+

4

a

取得最

小

小

值，为

4

4

；
（2）若a＞1，求代数式a+

25

a

-

1

的最小值；
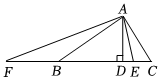
（3）如图，在△ABC中，∠BAC=90°，AB=a,AC=b,点E在BC上，且BE=AB，点F在CB延长线上，且BF=AC．已知△ABC的面积为

9

2

，求线段EF的最小值．