当前位置：试卷中心 > 试卷详情

2022-2023学年内蒙古赤峰市松山区赤峰红旗中学高一（下）期末数学试卷

发布：2024/7/13 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

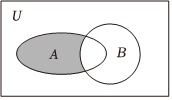1．若全集U=R，集合A={0，1，2，3，4，5}，B={x|x≥3}，则图中阴影部分表示的集合为（　　）
A．{3，4，5} B．{0，1，2} C．{0，1，2，3} D．{4，5}
组卷：102引用：2难度：0.8
解析
2．一个几何体有6个顶点，则这个几何体可能是（　　）
A．三棱柱 B．四棱锥 C．四棱柱 D．五棱台
组卷：163引用：3难度：0.8
解析
3．已知非零向量
a
，
b
，则“
a
•
b
=
0
”是“
a
⊥
b
”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：20引用：3难度：0.9
解析
4．若
2
sin
（
α
+
2022
π
）
-
cos
（
α
+
π
）
cos
（
α
-
3
π
2
）
-
3
cosα
=2，则
tan
（
α
+
π
4
）
=（　　）
A．
11
3
B．-
11
3
C．
3
11
D．-
3
11
组卷：246引用：4难度：0.8
解析
5．为落实党的二十大提出的“加快建设农业强国，扎实推动乡村振兴”的目标，银行拟在乡村开展小额贷款业务．根据调查的数据，建立了实际还款比例P关于还款人的年收入x（单位：万元）的Logistic模型：
P
（
x
）
=
e
-
0
.
9
+
kx
1
+
e
-
0
.
9
+
kx
．已知当贷款人的年收入为9万元时，其实际还款比例为50%．若银行希望实际还款比例为40%，则贷款人的年收入约为（　　）（参考数据：ln3≈1.1，ln2≈0.7）
A．4万元 B．8万元 C．6万元 D．5万元
组卷：34引用：3难度：0.6
解析
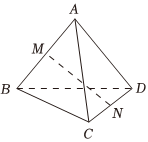6．空间四边形ABCD的对角线AC=2，
BD
=
2
2
，M、N分别为AB、CD的中点，MN=2，则异面直线MN与BD所成角的余弦值为（　　）
A．
2
2
B．
3
8
C．
3
2
D．
5
2
8
组卷：148引用：2难度：0.5
解析
7．已知某圆锥的侧面展开图是一个半径为r的半圆，且该圆锥的体积为
3
π
8
，则r=（　　）
A．
2
B．
3
C．3 D．2
组卷：29引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、演算步骤或证明过程．

21．某企业生产A，B两种产品，根据市场调查与预测，A产品的利润y与投资x成正比，其关系如图（1）所示；B产品的利润y与投资x的算术平方根成正比，其关系如图（2）所示（注：利润y与投资x的单位均为万元）．
（1）分别求A，B两种产品的利润y关于投资x的函数解析式；
（2）已知该企业已筹集到200万元资金，并将全部投入A，B两种产品的生产．
①若将200万元资金平均投入两种产品的生产，可获得总利润多少万元？
②如果你是厂长，怎样分配这200万元资金，可使该企业获得的总利润最大？其最大利润为多少万元？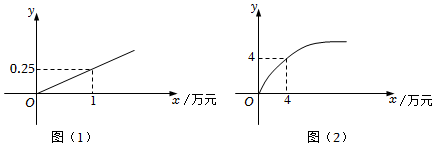
组卷：132引用：3难度：0.4
解析
22．已知函数h（x）=x²+bx+c是偶函数，且h（-1）=0，f（x）=
h
（
x
）
x
．
（Ⅰ）当x∈[1，2]时，求函数f（x）的值域；
（Ⅱ）设F（x）=x²+
1
x
2
-
2
a
（
x
-
1
x
）
，x∈[1，2]，求函数F（x）的最小值g（a）；
（Ⅲ）设t＜0，对于（Ⅱ）中的g（a），是否存在实数t,使得函数G（a）=log₂
a
3
+2a+tg（a）在
a
∈
（
1
，
3
2
）
时有且只有一个零点？若存在，求出实数t的取值范围；若不存在，请说明理由．
组卷：76引用：6难度：0.3
解析