2023-2024学年新疆乌鲁木齐101中高三（上）月考数学试卷（文科）（8月份）

一、单项选择题（共12小题每题5分共60分）

• 1．设集合A={x|x²-2x≤0}，B={-1，0，1，2，3}，则A∩B=（　　）

  A．{-1}

  B．{-1，0}

  C．{0，1}

  D．{0，1，2}
  组卷：128引用：4难度：0.8

  解析

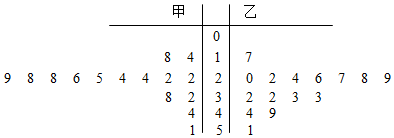• 2．如图所示的茎叶图记录了CBA球员甲、乙两人在2018-2019赛季某月比赛过程中的得分成绩，则下列结论正确的是（　　）

  A．甲的平均数大于乙的平均数

  B．甲的平均数小于乙的平均数

  C．甲的中位数大于乙的中位数

  D．甲的方差小于乙的方差
  组卷：90引用：2难度：0.9

  解析

• 3．若复数z满足（1-i）z=3+4i,则|z|=（　　）

  A． 5 2

  B． 5 2 2

  C． 2

  D．5
  组卷：155引用：6难度：0.9

  解析

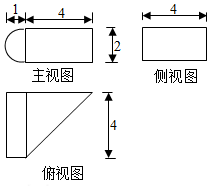• 4．某几何体由圆柱的部分和一个多面体组成，其三视图（单位：cm）如图所示，则该几何体的体积是（　　）cm³

  A．4π+32

  B．2π+32

  C．4π+16

  D．2π+16
  组卷：100引用：2难度：0.6

  解析

• 5．已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π），将f（x）图像上所有点向右平移

  π

  6

  ω

  个单位长度得到函数g（x）的图像，若g（x）是奇函数，f（x）在

  （

  0

  ，

  π

  6

  ）

  上单调递增，则ω的最大值为（　　）

  A． 2 3

  B．1

  C．2

  D．3
  组卷：105引用：7难度：0.6

  解析

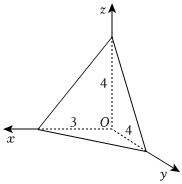• 6．如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的（左）侧视图是（　　）

  A．	B．
  C．	D．
  组卷：14引用：2难度：0.7

  解析

• 7．函数f（x）=（e^x+e^-x）ln|x|的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：76引用：6难度：0.8

  解析

三、解答题（共74分，请根据答题卡题号及分值在各题目的答题区域内作答，超出答题区域的答案无效。）

• 20．已知函数

  f

  （

  x

  ）

  =

  mlnx

  +

  1

  2

  x

  2

  -

  2

  x

  ．
  （1）若m＜0，曲线y=f（x）在点（1，f（1））处的切线在两坐标轴上的截距之和为2，求m的值；
  （2）若对于任意的

  m

  ∈

  [

  1

  2

  ，

  1

  ]

  及任意的x₁，x₂∈[2，e]，x₁≠x₂，总有

  |

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  |

  ＞

  t

  x

  1

  x

  2

  成立，求t的取值范围．
  组卷：161引用：5难度：0.1

  解析

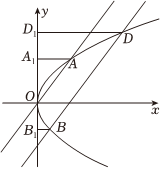• 21．已知点M（1，y）在抛物线C：y²=2px（p＞0）上，M点到抛物线C的焦点F的距离为2．
  （1）求抛物线C的方程；
  （2）已知直线l₁：x=my与抛物线C交于O（坐标原点）、A两点，直线l₂：x=my+m与抛物线C交于B、D两点．
  ①若|BD|=2|OA|，求实数m的值；
  ②过A、B、D分别作y轴的垂线，垂足分别为A₁、B₁、D₁．记S₁、S₂分别为三角形OAA₁和四边形BB₁D₁D的面积，求

  S

  1

  S

  2

  的取值范围．
  组卷：54引用：1难度：0.3

  解析