2023-2024学年四川省绵阳市涪城区南山中学实验学校高二（上）月考数学试卷（9月份）
发布：2024/9/9 16:0:8
一、单选题：本大题共8个小题，每个小题5分，共40分.在每个小题给出的四个选项中，只有一项是符合题目要求的.
-
1．在空间直角坐标系O-xyz中，点A（1，3，5）关于xOy平面的对称点B的坐标为（ ）
组卷：65引用：11难度：0.7 -
2．已知向量
，a=（1，-1，-2），则下列结论正确的是（ ）b=（1，-3，-3）组卷：112引用：13难度：0.8 -
3．袋内装有8个红球、2个白球，从中任取2个，其中是互斥而不对立的两事件是（ ）
组卷：422引用：3难度：0.9 -
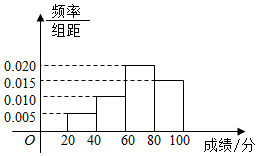4．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，若低于60分的人数是15人，则该班的学生人数是（ ）组卷：768引用：56难度：0.9 -
5．袋中有红色、黄色、绿色球各1个，每次任取1个，有放回地抽取三次，球的颜色全相同的概率是（ ）
组卷：47引用：6难度：0.9 -
6．在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A-BCD中，AB⊥平面BCD，BC⊥CD，且AB=BC=CD，M为AD的中点，则异面直线BM与CD夹角的余弦值为（ ）
组卷：336引用：22难度：0.6 -
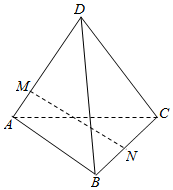7．已知四面体ABCD，=DA，a=DB，b=DC，点M在棱DA上，c=3DM，N为BC中点，则MA=（ ）MN组卷：683引用：9难度：0.7
四、解答题：本题共6个小题，共70分.解答应写出文字说明、证明过程或者演算步骤.
-
21．为了纪念中国古代数学家祖冲之在圆周率上的贡献，联合国教科文组织第四十届大会上把每年的3月14日定为“国际数学日”.2023年3月14日，某学校举行数学文化节活动，其中一项活动是数独比赛（注：数独是源自18世纪瑞士的一种数学游戏，又称九宫格）．甲、乙两位同学进入了最后决赛，进行数独王的争夺．决赛规则如下：进行两轮数独比赛，每人每轮比赛在规定时间内做对得1分，没做对得0分，两轮结束总得分高的为数独王，得分相同则进行加赛．根据以往成绩分析，已知甲每轮做对的概率为0.8，乙每轮做对的概率为0.75，且每轮比赛中甲、乙是否做对互不影响，各轮比赛甲、乙是否做对也互不影响．
（1）求两轮比赛结束乙得分为1分的概率；
（2）求不进行加赛甲就获得数独王的概率．组卷：211引用：5难度：0.7 -
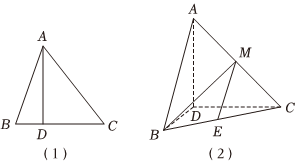22．条件①：图（1）中tan2B=-．条件②：图（1）中43=AD23+AB13．条件③：图（2）中三棱锥A-BCD的体积为AC．从以上三个条件中任选一个，补充在问题（2）中的横线上，并加以解答．如图（1）所示，在△ABC中，∠ACB=45°，BC=3，过点A作AD⊥BC，垂足D在线段BC上，沿AD将△ABD折起，使∠BDC=90°（如图（2）），点E，M分别为棱BC，AC的中点．23
（1）求证：CD⊥ME；
（2）已知_____，试在棱CD上确定一点N，使得EN⊥BM，并求二面角M-BN-C的余弦值．组卷：13引用：1难度：0.4
