2023-2024学年天津二十中高二(上)第一次统练数学试卷
发布:2024/9/11 3:0:8
一、单选题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1.已知向量
,则向量a=(1,2,2),b=(-2,1,1)在向量b上的投影向量为( )a组卷:811引用:12难度:0.7 -
2.已知直线l的倾斜角为
,直线l1经过点A(3,2)和B(a,-1),且直线l与l1垂直,则a的值为( )3π4组卷:284引用:9难度:0.8 -
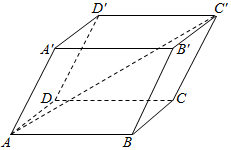 3.如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )组卷:258引用:14难度:0.7
3.如图,平行六面体ABCD-A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )组卷:258引用:14难度:0.7 -
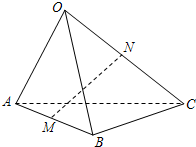 4.已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且=OA,a=OB,b=OC用c,a,b表示c,则MN等于( )MN组卷:1477引用:13难度:0.7
4.已知三棱锥O-ABC,点M,N分别为AB,OC的中点,且=OA,a=OB,b=OC用c,a,b表示c,则MN等于( )MN组卷:1477引用:13难度:0.7 -
5.在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E,F分别是CC1,AD的中点,那么异面直线OE和FD1所成角的余弦值等于( )
组卷:192引用:12难度:0.7 -
6.已知{
,a,b}是空间的一组基底,则可以与向量c=p+a,b=q-a构成基底的向量是( )b组卷:323引用:8难度:0.7
三、解答题(本大题共4小题,共36.0分。解答应写出文字说明,证明过程或演算步骤)
-
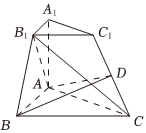 19.如图,在三棱台ABC-A1B1C1中,∠BAC=90°,AB=AC=4,A1A=A1B1=2,侧棱A1A⊥平面ABC,点D是棱CC1的中点.
19.如图,在三棱台ABC-A1B1C1中,∠BAC=90°,AB=AC=4,A1A=A1B1=2,侧棱A1A⊥平面ABC,点D是棱CC1的中点.
(1)证明:BB1⊥平面AB1C;
(2)求平面BCD与平面ABD的夹角的余弦值.组卷:106引用:6难度:0.6 -
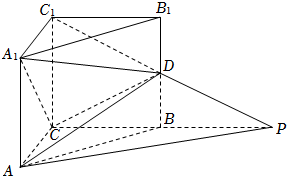 20.如图:在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,D是棱BB1的中点,P是C1D的延长线与CB的延长线的交点.
20.如图:在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=1,D是棱BB1的中点,P是C1D的延长线与CB的延长线的交点.
(1)求证:AP∥平面A1CD;
(2)求平面A1CD与平面A1C1D的夹角的余弦值;
(3)若点E在线段AP上,且直线A1E与平面A1CD所成的角的正弦值为,求线段AE的长.147组卷:150引用:2难度:0.5


