2023-2024学年湖北省云学新高考联盟学校高二（上）开学联考数学试卷（8月份）
发布：2024/8/28 4:0:8
一、单选题：本大题共8小题，每个小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.
-
1．容量为8的样本：3.5，3.8，4.2，4.8，5，5，5.5，6.3，其第75百分数是（ ）
组卷：52引用：5难度：0.7 -
2．在跳水比赛中，有8名评委分别给出某选手原始分，在评定该选手的成绩时，从8个原始分中去掉1个最高分和1个最低分，得到6个有效分，这6个有效分与8个原始分相比较，下列说法正确的是（ ）
组卷：283引用：10难度：0.7 -
3．在抛掷硬币试验中，记事件A为“正面朝上”，则下列说法正确的（ ）
组卷：125引用：6难度：0.8 -
4．在平行六面体ABCD-A1B1C1D1中，底面ABCD是菱形，侧面A1ADD1是正方形，且∠A1AB=120°，∠DAB=60°，AB=2，若P是C1D与CD1的交点，M是A1D1的中点，则MP=（ ）组卷：94引用：5难度：0.5 -
5．已知平面α⊥平面β，直线l⊄α，则“l⊥β”是“l∥α”的（ ）
组卷：295引用：9难度：0.5 -
6．圆台O1O2母线长为3，下底直径为10，上底直径为5，过圆台两条母线作截面，则该截面面积最大值为（ ）
组卷：56引用：3难度：0.8 -
7．二面角α-l-β中，A∈l,C∈l,AB⊂α，CD⊂β且AB⊥l,CD⊥l,垂足分别为A、C，AB=2，AC=1，CD=4，已知异面直线AB与CD所成角为60°，则BD=（ ）
组卷：160引用：1难度：0.5
四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.
-
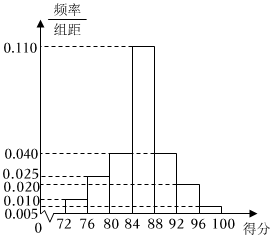21．插花是一种高雅的审美艺术，是表现植物自然美的一种造型艺术，与建筑、盆景等艺术形式相似，是最优美的空间造型艺术之一．为了通过插花艺术激发学生对美的追求，某校举办了以“魅力校园、花香溢校园”为主题的校园插花比赛．比赛按照百分制的评分标准进行评分，评委由10名专业教师、10名非专业教师以及20名学生会代表组成，各参赛小组的最后得分为评委所打分数的平均分．比赛结束后，得到甲组插花作品所得分数的频率分布直方图和乙组插花作品所得分数的频数分布表，如下所示：
定义评委对插花作品的“观赏值”如下所示：分数区间 频数 [72，76） 1 [76，80） 5 [80，84） 12 [84，88） 14 [88，92） 4 [92，96） 3 [96，100] 1
（1）估计甲组插花作品所得分数的中位数（结果保留两位小数）；分数区间 [72，84） [84，92） [92，100] 观赏值 1 2 3
（2）若该校拟从甲、乙两组插花作品中选出1个用于展览，从这两组插花作品的最后得分来看该校会选哪一组，请说明理由（同一组中的数据用该组区间的中点值作代表）；
（3）从40名评委中随机抽取1人进行调查，试估计其对乙组插花作品的“观赏值”比对甲组插花作品的“观赏值”高的概率．组卷：19引用：2难度：0.4 -
22．如图1，在△ABC中，BC=4，
，AB=13，E，D分别为BC，AC的中点，以DE为折痕，将△DCE折起，使点C到C1的位置，且BC1=2，如图2．cosB=1313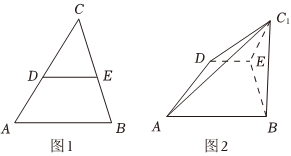
（1）设平面C1AD∩平面BEC1=1，证明：l⊥平面ABC1；
（2）P是棱C1D上一点（不含端点）过P、B、E三点作该四棱锥的截面，要求保留画痕，并说明过程；
（3）若（2）中的截面与面BEC1所成的二面角的正切值为，求该截面将四棱锥分成上下两部分的体积之比．32组卷：46引用：4难度：0.4
