2022-2023学年山东省德州市乐陵市七年级（下）期中数学试卷

一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确得选项选出来，每小题选对得4分，选错、不选或选出得答案超过一个均记零分．

• 1．下列图形中∠1和∠2是对顶角的是（　　）

  A．	B．
  C．	D．
  组卷：245引用：12难度：0.8

  解析

• 2．如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（　　）

  A．两直线平行，同位角相等

  B．同旁内角互补，两直线平行

  C．内错角相等，两直线平行

  D．同位角相等，两直线平行
  组卷：313引用：10难度：0.9

  解析

• 3．下列四个选项，能通过平移得到的图案是（　　）#ZZ04

  A．

  B．

  C．

  D．
  组卷：9引用：2难度：0.5

  解析

• 4．“9的平方根”这句话用数学符号表示为（　　）

  A． 9

  B． ± 9

  C． 3

  D． ± 3
  组卷：821引用：5难度：0.9

  解析

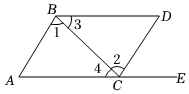• 5．如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AC的是（　　）

  A．∠3=∠4	B．∠1=∠2
  C．∠D=∠DCE	D．∠D+∠ACD=180°
  组卷：1331引用：33难度：0.7

  解析

• 6．在下列实数中，属于无理数的是（　　）

  A． 4

  B． 2

  C． 3 27

  D． 22 7
  组卷：51引用：5难度：0.9

  解析

• 7．已知a是正整数，且满足a-1＜

  56

  ＜a,则a的值是（　　）

  A．9

  B．8

  C．7

  D．6
  组卷：123引用：2难度：0.8

  解析

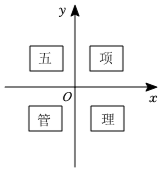• 8．教育部办公厅中小学2021下发了“五项管理”文件．小明将写有“五项管理”的四张卡片分别放入平面直角坐标系中，如图，“管”字卡片遮住的坐标可能是（　　）

  A．（-2，-3）

  B．（-2，3）

  C．（2，-3）

  D．（2，3）
  组卷：197引用：3难度：0.7

  解析

三、解答题（本大题共8小题，共78分）

• 25．问题情境：
  在平面直角坐标系xOy中有不重合的两点A（x₁，y₁）和点B（x₂，y₂），小明在学习中发现，若x₁=x₂，则AB∥y轴，且线段AB的长度为|y₁-y₂|；若y₁=y₂，则AB∥x轴，且线段AB的长度为|x₁-x₂|；
  【应用】：
  （1）若点A（-1，1）、B（2，1），则AB∥x轴，AB的长度为

  ．
  （2）若点C（1，0），且CD∥y轴，且CD=2，则点D的坐标为

  ．
  【拓展】：
  我们规定：平面直角坐标系中任意不重合的两点M（x₁，y₁），N（x₂，y₂）之间的折线距离为d（M，N）=|x₁-x₂|+|y₁-y₂|；例如：图1中，点M（-1，1）与点N（1，-2）之间的折线距离为d（M，N）=|-1-1|+|1-（-2）|=2+3=5．
  解决下列问题：
  （1）如图2，已知E（2，0），若F（-1，-2），则d（E，F）

  ；
  （2）如图2，已知E（2，0），H（1，t），若d（E，H）=3，则t=

  ．
  （3）如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，则d（P，Q）=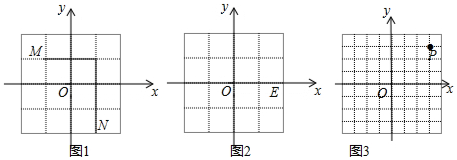

  ．
  
  组卷：6701引用：35难度：0.5

  解析

• 26．【阅读理解】
  我们经常过某个点作已知直线的平行线，以便利用平行线的性质来解决问题．
  例如：如图1，AB∥CD，点E、F分别在直线AB、CD上，点P在直线AB、CD之间，设∠AEP=∠α，∠CFP=∠β，求证：∠P=∠α+∠β．
  证明：如图2，过点P作PQ∥AB，
  ∴∠EPQ=∠AEP=∠α，
  ∵PQ∥AB，AB∥CD，
  ∴PQ∥CD，
  ∴∠FPQ=∠CFP=∠β，
  ∴∠EPF=∠EPQ+∠FPQ=∠α+∠β．
  即∠P=∠α+∠β．
  可以运用以上结论解答下列问题：
  【类比应用】
  （1）如图3，已知AB∥CD，已知∠D=40°，∠GAB=60°，求∠P的度数；
  （2）如图4，已知AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA、PE．设∠A=∠α、∠CEP=∠β，则∠α、∠β、∠P之间有何数量关系？请说明理由；
  【拓展应用】
  （3）如图5，已知AB∥CD，点E在直线CD上，点P在直线AB上方，连接PA、PE，∠PED的角平分线与∠PAB的角平分线所在直线交于点Q，求

  1

  2

  ∠

  P

  +

  ∠

  Q

  的度数．
  组卷：388引用：4难度：0.6

  解析