2022-2023学年云南省昆明市嵩明县高二（上）期中数学试卷

一、单选题。本大题共8个小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项符合题目要求，请在答题卡相应的位置上填涂。

• 1．设集合M={-1，0，2}，N={0，2，3}，M∪N=（　　）

  A．{0，2}

  B．{-1，2，3}

  C．{-1，0，3}

  D．{-1，0，2，3}
  组卷：1引用：1难度：0.8

  解析

• 2．直线

  y

  =

  3

  x

  的倾斜角为（　　）

  A．60°

  B．90°

  C．120°

  D．不存在
  组卷：21引用：7难度：0.9

  解析

• 3．圆x²+y²-4x+6y=0的圆心坐标是（　　）

  A．（-2，3）

  B．（2，3）

  C．（-2，-3）

  D．（2，-3）
  组卷：1162引用：46难度：0.9

  解析

• 4．已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是平行四边形，且

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  B

  D

  1

  =（　　）

  A． a + b + c

  B． a - b + c

  C．- a + b + c

  D．- a + b - c
  组卷：67引用：4难度：0.7

  解析

• 5．已知

  sin

  （

  3

  π

  +

  α

  ）

  =

  3

  5

  ，且α在第三象限，则cosα=（　　）

  A． - 4 5

  B． - 3 5

  C． 3 5

  D． 4 5
  组卷：32引用：3难度：0.7

  解析

• 6．已知直线x-y+2=0与圆（x-1）²+（y-2）²=4交于A，B两点，则|AB|=（　　）

  A． 14

  B． 15

  C． 2 3

  D．4
  组卷：18引用：3难度：0.6

  解析

• 7．某市共享电动车2017年投放量为400万辆，根据前期市场调研，为满足市场需求，以后每一年的投放量都比上一年提高20%，那么该市到哪一年共享电动车的投放量才能达到1200万辆（参考数据：lg1.2≈0.08，lg3≈0.48）（　　）

  A．2022年

  B．2023年

  C．2024年

  D．2025年
  组卷：84引用：2难度：0.5

  解析

四、解答题。本大题有6个小题，共70分。解答应写出文字说明、证明过程或演算过程。

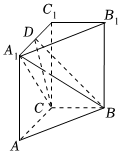• 21．在直三棱柱ABC-A₁B₁C₁中，平面A₁BC⊥平面AA₁C₁C．
  （1）求证AC⊥BC；
  （2）AC=BC=2，AA₁=3，D为A₁C₁的中点，求二面角A₁-BC-D的余弦值．
  ​
  组卷：7引用：1难度：0.5

  解析

• 22．已知圆心为C的圆经过A（3，0），B（-1，4）两点，且圆心在直线l₁：y=3x-1上．
  （1）求圆C的方程；
  （2）在直线l₂：y=-2x上是否存在一点Q，过点Q向圆C引两切线，切点为E，F，使△QEF为正三角形，若存在，求出点Q的坐标，若不存在，说明理由．
  组卷：21引用：3难度：0.6

  解析