2022-2023学年四川省眉山市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．复数

  6

  （

  cos

  4

  π

  3

  +

  isin

  4

  π

  3

  ）

  =（　　）

  A． - 3 - 3 3 i

  B． - 3 3 - 3 i

  C． - 3 + 3 3 i

  D． 3 - 3 3 i
  组卷：13引用：5难度：0.8

  解析

• 2．数据1，2，3，4，5，6，7，8的60%分位数为（　　）

  A．4.5

  B．5

  C．5.5

  D．6
  组卷：42引用：5难度：0.8

  解析

• 3．已知α是第二象限角，那么

  α

  2

  是（　　）

  A．第一象限角	B．第二象限角
  C．第二或第四象限角	D．第一或第三象限角
  组卷：845引用：33难度：0.9

  解析

• 4．能使平面α与平面β平行的一个条件是（　　）

  A．α与β都平行于同一条直线

  B．一条直线l分别与α和β所成的角相等

  C．α内有无数条直线都与β平行

  D．α内的任何一条直线都与β平行
  组卷：163引用：4难度：0.9

  解析

• 5．sin105°sin15°-cos105°cos15°的值为（　　）

  A． 3 2

  B． 1 2

  C．0

  D． - 1 2
  组卷：118引用：6难度：0.8

  解析

• 6．在△ABC中，内角A，B，C的对边分别为a,b,c,已知B=30°，

  b

  =

  2

  ，c=2，则（　　）

  A．C=45°	B．A=15°
  C． a = 3 - 1	D．△ABC为钝角三角形
  组卷：53引用：3难度：0.6

  解析

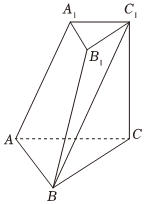• 7．三棱台ABC-A₁B₁C₁中，两底面△ABC和△A₁B₁C₁分别是边长为2和1的等边三角形，CC₁⊥平面ABC．若CC₁=2，则异面直线AC与BC₁所成角的余弦值为（　　）

  A． 14 4

  B． 7 7

  C． 2 4

  D． 2 2
  组卷：161引用：8难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．在△ABC中，点P为△ABC所在平面内一点．
  （1）若点P在边BC上，且

  BP

  =

  1

  3

  PC

  ，用

  AB

  ，

  AC

  表示

  AP

  ；
  （2）若点P是△ABC的重心．
  ①求证：

  PA

  +

  PB

  +

  PC

  =

  0

  ；
  ②若

  35

  sin

  A

  •

  PA

  +

  21

  sin

  B

  •

  PB

  +

  15

  sin

  C

  •

  PC

  =

  0

  ，求cos∠BAC．
  组卷：50引用：6难度：0.5

  解析

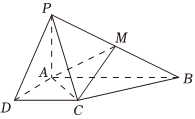• 22．已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中点．
  （1）证明：BC⊥平面PAC；
  （2）判断直线CM与平面PAD的位置关系，并证明你的结论；
  （3）求二面角A-MC-B的余弦值．
  组卷：294引用：9难度：0.5

  解析