2023-2024学年天津市北辰区朱唐庄中学高三（上）第一次月考数学试卷（10月份）

一、单项选择（每题5分，共60分。每题仅有一个正确选项，请将正确选项写到答题卡上）

• 1．已知U={0，1，2，3，4，5，6}，A={1，3，5}，B={2，4，5}，则A∩（∁_UB）（　　）

  A．{1，3，5}

  B．{1，3}

  C．{2，4，6}

  D．{0，2，4，6}
  组卷：46引用：1难度：0.9

  解析

• 2．设集合A={0，1，2，3}，B={1，3，4}，C={x∈R|x²-3x+2＞0}，则（A∪B）∩C=（　　）

  A．{3}

  B．{1，2}

  C．{1，3}

  D．{0，3，4}
  组卷：350引用：4难度：0.7

  解析

• 3．已知全集U={x∈Z|x²-5x-6≤0}，集合A={x∈Z|x（2-x）≥0}，集合B={1，2，3}，则集合∁_U（A∪B）=（　　）

  A．{1，2}	B．{0，1，2，3}
  C．{-1，0，3，4，5，6}	D．{-1，4，5，6}
  组卷：339引用：6难度：0.7

  解析

• 4．已知p：0＜x＜2，q：-1＜x＜3，则p是q的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：800引用：42难度：0.9

  解析

• 5．已知a≠0，命题p：x=1是一元二次方程ax²+bx+c=0的一个根，命题q：a+b+c=0，则p是q的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：418引用：5难度：0.7

  解析

• 6．设x∈R，则“

  x

  -

  5

  2

  -

  x

  ＞

  0

  ”是“|x-1|＜4”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：47引用：2难度：0.7

  解析

• 7．下列可能是函数

  y

  =

  x

  2

  -

  1

  e

  x

  2

  的图象的是（　　）

  A．	B．
  C．	D．
  组卷：42引用：1难度：0.8

  解析

三、解答题（每题15分，共60分）

• 21．已知底面ABCD是正方形，PA⊥平面ABCD，PA∥DQ，PA=AD=3DQ=3，点E、F'分别为线段PB、CQ的中点．
  （1）求证：EF∥平面PADQ；
  （2）求直线EF与平面PCQ夹角的正弦值；
  （3）求点F到面PAC的距离．
  组卷：44引用：1难度：0.5

  解析

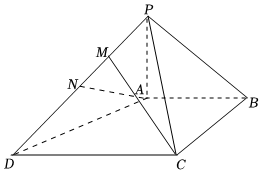• 22．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB∥CD，且CD=2，AB=1，

  BC

  =

  2

  2

  ，

  PA

  =

  1

  ，

  AB

  ⊥

  BC

  ，

  N

  为PD的中点．
  （1）求平面PAD与平面PBC所成锐二面角的余弦值；
  （2）求点N到直线BC的距离；
  （3）在线段PD上是否存在一点M，使得直线CM与平面PBC所成角的正弦值为

  26

  26

  ，若存在，求出

  DM

  DP

  的值；若不存在，说明理由．
  组卷：299引用：4难度：0.4

  解析