当前位置：试卷中心 > 试卷详情

2023-2024学年北京166中高三（上）诊断数学试卷（10月份）

发布：2024/9/7 6:0:11

一、单选题（共10题，每题4分）

1．设集合A={x∈Z|-2＜x≤1}，B={0，1，2}，则A∩B=（　　）
A．{-1，0，1，2} B．{0，1}
C．{-2，-1，0，1，2} D．{0，1，2}
组卷：126引用：6难度：0.9
解析
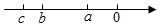2．已知实数a,b,c在数轴上对应的点如图所示，则下列式子中正确的是（　　）
A．b-a＜c+a B．c²＜ab C．
c
b
＞
c
a
D．|b|c＜|a|c
组卷：142引用：11难度：0.5
解析
3．下列函数中，值域为R且在区间（0，+∞）上单调递增的是（　　）
A．y=x²+2x B．y=2^x+1 C．y=x³+1 D．y=（x-1）|x|
组卷：1372引用：13难度：0.8
解析
4．在△ABC中，
（
a
-
c
）
（
sin
A
+
sin
C
）
=
（
a
+
b
）
cos
（
π
2
+
B
）
，则∠C=（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
组卷：192引用：2难度：0.5
解析
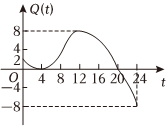5．老舍在《济南的冬天》中写到济南的冬天是没有风声的，济南的冬天是响晴的，济南真得算个宝地．济南市某一天内的气温Q（t）（单位：℃）与时刻t（单位：时）之间的关系如图所示，令C（t）表示时间段[0，t]内的温差（即时间段[0，t]内最高温度与最低温度的差），C（t）与t之间的函数关系用下列图象表示，则下列正确的图象是（　　）
A． B．
C． D．
组卷：13引用：1难度：0.7
解析
6．已知定义在R上的奇函数f（x）在（-∞，0）上单调递减且f（-1）=0，若a=f（-log₃8），b=f（-log₂4），c=f（
2
2
3
），则a,b,c的大小关系是（　　）
A．c＜a＜b B．a＜b＜c C．a＜c＜b D．c＜b＜a
组卷：40引用：3难度：0.6
解析
7．已知函数f（x）=2cos²（x+θ）-1，则“
θ
=
π
4
+
kπ

（
k
∈
Z
）
”是“f（x）为奇函数”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：295引用：4难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共6题，每题85分）

20．已知函数f（x）=2lnx-x-lna,a＞0．
（Ⅰ）求曲线y=f（x）在（1，f（1））处切线的斜率；
（Ⅱ）求函数f（x）的极大值；
（Ⅲ）设g（x）=ae^x-x²，当a∈（1，e）时，求函数g（x）的零点个数，并说明理由．
组卷：561引用：6难度：0.4
解析
21．设A是由m×n个实数组成的m行n列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．
（Ⅰ）数表A如表1所示，若经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负实数，请写出每次“操作”后所得的数表（写出一种方法即可）；

1 2 3 -7

-2 1 0 1

表1
（Ⅱ）数表A如表2所示，若必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和均为非负整数，求整数a的所有可能值；

a a²-1 -a -a²

2-a 1-a² a-2 a²

表2
（Ⅲ）对由m×n个实数组成的m行n列的任意一个数表A，能否经过有限次“操作”以后，使得到的数表每行的各数之和与每列的各数之和均为非负整数？请说明理由．
组卷：199引用：7难度：0.1
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．{-1，0，1，2}	B．{0，1}
C．{-2，-1，0，1，2}	D．{0，1，2}

A．充分而不必要条件	B．必要而不充分条件
C．充分必要条件	D．既不充分也不必要条件

A．	B．
C．	D．

a	a²-1	-a	-a²
2-a	1-a²	a-2	a²

2023-2024学年北京166中高三（上）诊断数学试卷（10月份）

一、单选题（共10题，每题4分）

1．设集合A={x∈Z|-2＜x≤1}，B={0，1，2}，则A∩B=（ ）

2．已知实数a,b,c在数轴上对应的点如图所示，则下列式子中正确的是（ ）

3．下列函数中，值域为R且在区间（0，+∞）上单调递增的是（ ）

4．在△ABC中，（a-c）（sinA+sinC）=（a+b）cos（π2+B），则∠C=（ ）

6．已知定义在R上的奇函数f（x）在（-∞，0）上单调递减且f（-1）=0，若a=f（-log38），b=f（-log24），c=f（223），则a,b,c的大小关系是（ ）

7．已知函数f（x）=2cos2（x+θ）-1，则“θ=π4+kπ （k∈Z）”是“f（x）为奇函数”的（ ）

三、解答题（共6题，每题85分）

20．已知函数f（x）=2lnx-x-lna,a＞0．（Ⅰ）求曲线y=f（x）在（1，f（1））处切线的斜率；（Ⅱ）求函数f（x）的极大值；（Ⅲ）设g（x）=aex-x2，当a∈（1，e）时，求函数g（x）的零点个数，并说明理由．

1．设集合A={x∈Z|-2＜x≤1}，B={0，1，2}，则A∩B=（　　）

2．已知实数a,b,c在数轴上对应的点如图所示，则下列式子中正确的是（　　）

3．下列函数中，值域为R且在区间（0，+∞）上单调递增的是（　　）

4．在△ABC中，
（
a
-
c
）
（
sin
A
+
sin
C
）
=
（
a
+
b
）
cos
（
π
2
+
B
）
，则∠C=（　　）

6．已知定义在R上的奇函数f（x）在（-∞，0）上单调递减且f（-1）=0，若a=f（-log₃8），b=f（-log₂4），c=f（
2
2
3
），则a,b,c的大小关系是（　　）

7．已知函数f（x）=2cos²（x+θ）-1，则“
θ
=
π
4
+
kπ

（
k
∈
Z
）
”是“f（x）为奇函数”的（　　）

20．已知函数f（x）=2lnx-x-lna,a＞0．
（Ⅰ）求曲线y=f（x）在（1，f（1））处切线的斜率；
（Ⅱ）求函数f（x）的极大值；
（Ⅲ）设g（x）=ae^x-x²，当a∈（1，e）时，求函数g（x）的零点个数，并说明理由．