2023年辽宁省锦州市中考数学二模试卷
发布:2024/7/14 8:0:9
一、选择题(本大题共8个小题,每小题2分,共16分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.-2023的绝对值是( )
组卷:2248引用:157难度:0.9 -
2.下列交通标志是轴对称图形的是( )
组卷:161引用:7难度:0.9 -
3.下列运算正确的是( )
组卷:57引用:1难度:0.7 -
4.下列事件是必然事件的是( )
组卷:153引用:1难度:0.7 -
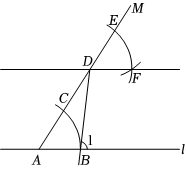 5.如图,点A在直线l上,(1)过点A作射线AM;(2)以点A为圆心,以任意长为半径作弧交直线l于点B,交射线AM于点C;(3)在射线CM上取一点D,以点D为圆心,以AB长为半径作弧交射线DM于点E;(4)以点E为圆心,以CB长为半径作弧交前面的弧于点F;(5)作直线DF,连接BD.若∠EDF=54°,∠ADB=30°,则∠1的度数为( )#ZZ04组卷:170引用:1难度:0.5
5.如图,点A在直线l上,(1)过点A作射线AM;(2)以点A为圆心,以任意长为半径作弧交直线l于点B,交射线AM于点C;(3)在射线CM上取一点D,以点D为圆心,以AB长为半径作弧交射线DM于点E;(4)以点E为圆心,以CB长为半径作弧交前面的弧于点F;(5)作直线DF,连接BD.若∠EDF=54°,∠ADB=30°,则∠1的度数为( )#ZZ04组卷:170引用:1难度:0.5 -
6.为创建文明城市,减少施工对环境造成的影响,某施工队在小区里对一段全长为300米的地下管线进行修复时,实际每天的工作效率比原计划提高了20%,结果提前2天完成修复任务.求实际每天修复管线多少米?设原计划每天修复管线x米,则可列方程为( )
组卷:155引用:1难度:0.7 -
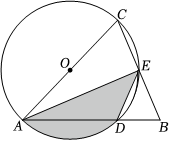 7.如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为( )组卷:2410引用:14难度:0.7
7.如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若∠BED=45°,AB=2,则阴影部分的面积为( )组卷:2410引用:14难度:0.7 -
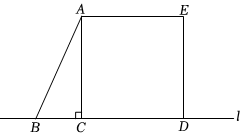 8.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AC=2cm,以AC为边向外作正方形ACDE,将△ABC以1cm/s的速度沿BC所在的直线l向右移动,直到点B与点D重合时停止移动.设运动时间为x s,△ABC与正方形ACDE重叠部分的面积为y cm2,则下列图象能大致反映y与x之间函数关系的是( )3组卷:165引用:2难度:0.4
8.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AC=2cm,以AC为边向外作正方形ACDE,将△ABC以1cm/s的速度沿BC所在的直线l向右移动,直到点B与点D重合时停止移动.设运动时间为x s,△ABC与正方形ACDE重叠部分的面积为y cm2,则下列图象能大致反映y与x之间函数关系的是( )3组卷:165引用:2难度:0.4
七、解答题(本题共12分)
-
24.【问题情境】如图1,在△ABC中,∠ACB=90°,AC=BC,D,E是AB上的两个动点,且AD=BE,连接CD,CE.
【初步尝试】
(1)∠ACD与∠BCE之间的数量关系 ;
【深入探究】
(2)如图2,点F在边BC上,且DF=DC,CE与DF相交于点G.
①求证:DF⊥CE;
②探究线段CF与BE之间的数量关系,并说明理由;
【拓展应用】
(3)如图3,在△ABC中,∠ACB=90°,AC=BC,点D,E分别在线段AB两侧的延长线上,且AD=BE,连接CD,CE.点F在边BC的延长线上,且DF=DC,EC的延长线与DF相交于点G.若AC=3,AD=,请直接写出CG的长度.2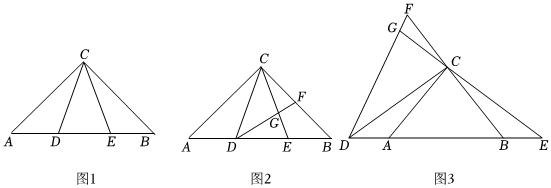 组卷:467引用:1难度:0.4
组卷:467引用:1难度:0.4
八、解答题(本题共12分)
-
25.如图,在平面直角坐标系中,二次函数
的图象与坐标轴分别交于A,B,C三点,其中点A的坐标为(-4,0),点B的坐标为(8,0).y=-14x2+bx+c
(1)求抛物线的表达式;
(2)点D的坐标为(0,4),P是x轴下方抛物线上的一个动点,连接AC,BD,PD,PB.若S△PBD=S△AOC,求点P的坐标;32
(3)在(2)的条件下,P是第四象限内的定点,Q为y轴上一个动点,则是否存在最小值?如果存在,求出这个最小值;如果不存在,请说明理由.5PQ+CQ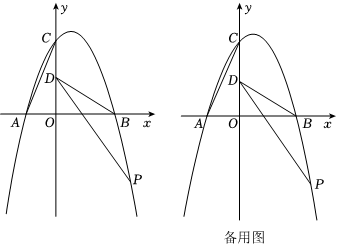 组卷:357引用:1难度:0.1
组卷:357引用:1难度:0.1


