当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省镇江市丹徒区八年级（下）期末数学试卷

发布：2024/7/5 8:0:9

一、填空题（本大题共有12小题，每小题2分，共计24分．）

1．使式子
4
-
x
有意义的x的取值范围是

．
组卷：225引用：31难度：0.7
解析
2．当x=
时，分式
x
-
2
x
-
1
的值为0．
组卷：148引用：7难度：0.8
解析
3．在平行四边形ABCD中，∠A与∠B的度数之比为2：1，则∠C=
．
组卷：840引用：11难度：0.8
解析
4．有若干个数据，最大值是134，最小值是103．用频数分布表描述这组数据时，若取组距为4，则应分为
组．
组卷：60引用：1难度：0.7
解析
5．已知一个菱形的边长为5，其中一条对角线长为8，则这个菱形的面积为
．
组卷：718引用：20难度：0.7
解析
6．已知|a-2|+
2
b
-
1
=0，则ab=
．
组卷：70引用：1难度：0.8
解析
7．若反比例函数y=
2
-
k
x
的图象位于第二、四象限，则k的取值范围是
．
组卷：1915引用：32难度：0.9
解析
8．点P₁（x₁，y₁），P₂（x₂，y₂），P₃（x₃，y₃）是反比例函数
y
=
a
x
（
a
＞
0
）
的图象上三点，且y₁＜y₂＜0＜y₃，则x₁，x₂，x₃的大小关系是
.（用“＜”连接）．
组卷：139引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共有8小题，共计78分．解答时应写出必要的文字说明、证明过程或演算步骤．）

25．我们可以通过剪纸、拼图等方式，更好的理解二次根式．请完成下列任务：
任务一：
如图1，有两张边长为a的正方形纸片，将其各剪一刀进行分割，再拼成一个新的正方形，要求：拼接时图形没有重合，图形间也没有空隙．
（1）请在图1的两个小正方形中画出分割线，然后在虚线框中画出拼成的新的正方形；
（2）由（1）中的操作可知，两张边长为a的正方形纸片面积和为
，我们所拼成的新的正方形的边长为
；
任务二：
在一张长方形纸片的顶点处剪去一个小长方形，得到图2，已知AB=AF=a,DC=DE=b.
（1）尝试将图2所示的纸片分割并拼成一个新的大正方形，要求：拼接时图形没有重合，图形间也没有空隙．请直接在图2中画出分割线和拼成的正方形；
（2）点G是图2中的BC边的中点，设点D到直线AG的距离为h,求证：h=
（
a
+
b
）
2
5
a
2
+
b
2
+
2
ab
5
a
2
+
b
2
+
2
ab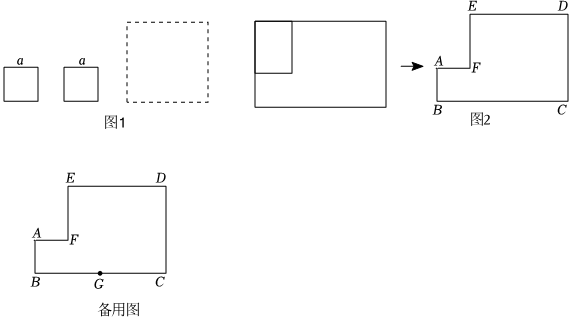
．
组卷：110引用：1难度：0.6
解析
26．【材料一】如果一个函数图象关于某点对称，就称这个函数为“和美函数”．例如反比例函数
y
=
k
x
（
k
≠
0
）
的图象关于原点O对称，所以反比例函数
y
=
k
x
（
k
≠
0
）
是“和美函数”．
【材料二】我们知道，一次函数y=x-1的图象可以由正比例函数y=x的图象向下平移一个单位得到．
根据上述材料，请你完成下列探究：
（1）函数
y
=
1
x
+
1
可以由函数
y
=
1
x
向
（填“左”或“右”）平移
个单位得到，因此函数
y
=
1
x
+
1
也是“和美函数”，它的对称点的坐标为
；
（2）一次函数y₁=kx+b的图象经过“和美函数”
y
2
=
x
+
2
x
+
1
的对称点，并且与“和美函数”
y
2
=
x
+
2
x
+
1
的图象交于点A（0，2）、点B．
①当y₁＜y₂时，求出x的取值范围；
②是否存在过原点的直线l,使得“和美函数”
y
2
=
x
+
2
x
+
1
关于直线l对称？如果存在，求出直线l对应的一次函数表达式；如果不存在，说明理由．
组卷：578引用：4难度：0.4
解析