2021-2022学年四川省泸州市高二（下）期末数学试卷（文科）

一、选择题：本大题共有12个小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合要求的．

• 1．复数

  2

  i

  1

  -

  i

  的虚部为（　　）

  A．i

  B．-i

  C．1

  D．-1
  组卷：31引用：5难度：0.8

  解析

• 2．命题“∀x∈R，sinx+1≥0”的否定是（　　）

  A．∃x0∈R，sinx0+1＜0	B．∀x∈R，sinx+1＜0
  C．∃x0∈R，sinx0+1≥0	D．∀x∈R，sinx+1≤0
  组卷：231引用：14难度：0.8

  解析

• 3．已知直线l₁：ax-4y-3=0，l₂：x-ay+1=0，则“l₁∥l₂”是“a=2”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：97引用：4难度：0.7

  解析

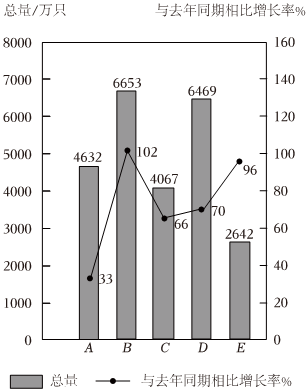• 4．在新冠肺炎疫情期间，各口罩企业都加大了生产力度，如图是2022年第一季度五个企业的生产量情况，则下列叙述正确的是（　　）

  A．2022年第一季度生产总量的增长率由低到高排位第5的是E企业

  B．2022年第一季度生产总量和增速由高到低排位均居同一位次的企业只有一个

  C．2021年同期C企业的生产总量不超过2000万只

  D．与2021年同期相比，各企业2022年第一季度的生产总量都实现了增长
  组卷：7引用：3难度：0.8

  解析

• 5．某厂在生产某产品的过程中，采集并记录了产量x（吨）与生产能耗y（吨）的下列对应数据：根据表中数据，用最小二乘法求得回归直线方程

  ̂

  y

  =

  ̂

  b

  x+1.5．那么据此回归模型可预测当产量为7吨时生产能耗约为（　　）
  

  x	2	4	6	8
  y	3	4	6	7

  A．4.625吨

  B．4.9375吨

  C．5吨

  D．6.4吨
  组卷：14引用：3难度：0.5

  解析

• 6．在区间（0，6）内任取一个实数m,使不等式m²-4m+3＜0的概率是（　　）

  A． 1 3

  B． 1 2

  C． 1 4

  D． 2 3
  组卷：5引用：2难度：0.8

  解析

• 7．已知H_n=1+

  1

  2

  +

  1

  3

  +

  ⋯

  +

  1

  n

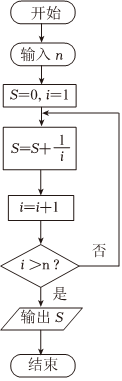  通常被称为“调和级数”，是级数理论中最早被人们研究的级数之一．著名数学家欧拉在1734年就曾给出证明：H_n≈ln（n+1）+α，其中α为欧拉-马歇罗尼常数，其值约为0.57．根据此式，如图所示的程序框图中，当输入的n为80时，输出结果S约为（　　）（参考数据：ln3≈1.10）

  A．3.87

  B．4.40

  C．4.97

  D．3.30
  组卷：3引用：3难度：0.8

  解析

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.

• 22．已知曲线C₁的参数方程为

  x = e t + e - t

  y = e t - e - t

  （t为参数），以直角坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C₂的极坐标方程ρ=4cosθ．
  （1）求C₁的极坐标方程；
  （2）若曲线

  θ

  =

  π

  6

  （

  ρ

  ＞

  0

  ）

  与曲线C₁、曲线C₂分别交于两点A，B，点P（4，0），求△PAB的面积．
  组卷：88引用：5难度：0.6

  解析

• 23．选修4-5：不等式选讲
  已知函数f（x）=x-

  1

  2

  ，g（x）=2x-4．
  （Ⅰ）若|f（x）+g（x）|=|f（x）|+|g（x）|，求x的取值范围；
  （Ⅱ）若|2f（x）|+|g（x）|的最小值为m,且正实数a,b,c,满足a+2b-m=-3c,证明：

  1

  a

  +

  c

  +

  2

  b

  +

  c

  ≥3．
  组卷：3引用：2难度：0.5

  解析