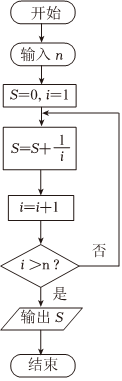
已知Hn=1+12+13+⋯+1n通常被称为“调和级数”，是级数理论中最早被人们研究的级数之一．著名数学家欧拉在1734年就曾给出证明：Hn≈ln（n+1）+α，其中α为欧拉-马歇罗尼常数，其值约为0.57．根据此式，如图所示的程序框图中，当输入的n为80时，输出结果S约为（ ）（参考数据：ln3≈1.10）
1
2
+
1
3
+
⋯
+
1
n
【考点】程序框图．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/6 8:0:9组卷：3引用：3难度：0.8
相似题
-
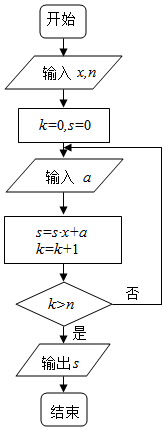1．中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=3，n=3，输入的a依次为由小到大顺序排列的质数（从最小质数开始），
直到结束为止，则输出的s=（ ）发布：2025/1/3 8:0:1组卷：10引用：1难度：0.7 -
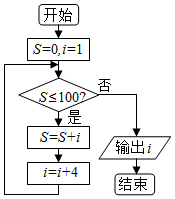2．执行如图所示的程序框图，则输出的i=（ ）发布：2024/12/30 10:0:5组卷：40引用：1难度：0.8 -
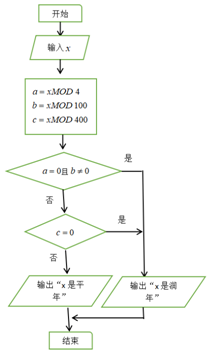3．如图是判断输入的年份x是否是闰年的程序框图，若先后输入x=1900，x=2400，则输出的结果分别是（注：xMODy表示x除以y的余数）（ ）发布：2025/1/15 8:0:2组卷：25引用：3难度：0.7
