当前位置：试卷中心 > 试卷详情

2022-2023学年河南省信阳高级中学高一（上）月考数学试卷（1月份）（一）

发布：2024/7/22 8:0:9

一、单选题（本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．下列函数中，其定义域和值域分别与函数y=e^lnx的定义域和值域相同的是（　　）
A．y=x B．y=lnx C．y=e^x D．
y
=
1
x
组卷：386引用：5难度：0.8
解析
2．已知ab=-5，则
a
-
b
a
+
b
-
a
b
的值是（　　）
A．
2
5
B．0 C．
-
2
5
D．
±
2
5
组卷：1465引用：6难度：0.7
解析
3．区块链作为一种新型的技术，已经被应用于许多领域．在区块链技术中，某个密码的长度设定为512B，则
密码一共有2⁵¹²种可能，为了破解该密码，最坏的情况需要进行2⁵¹²次运算．现在有一台计算机，每秒能进行1.25×10¹³次运算，那么在最坏的情况下，这台计算机破译该密码所需时间大约为（　　）
（参考数据：lg2≈0.3，
10
≈
3
.
16
）
A．6.32×10¹⁴¹s B．6.32×10¹⁴⁰s
C．3.16×10¹⁴¹s D．3.16×10¹⁴⁰s
组卷：297引用：11难度：0.5
解析
4．已知a=sin53°，b=log₅2，c=0.5^0.8，则a,b,c的大小关系为（　　）
A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b
组卷：58引用：4难度：0.6
解析
5．已知函数
f
（
x
）
=
lo
g
a
|
x
+
m
|
2
x
2
+
b
的图象如图所示，当x＜n时，有f（x）＞0，则下列判断中正确的是（　　）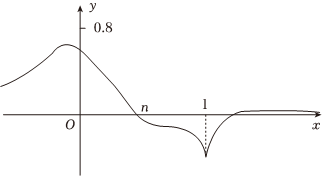
A．a＞1，m＞0，b＜0 B．a＞1，m＜0，b＞0
C．0＜a＜1，m＜0，b＞0 D．0＜a＜1，m＜0，b＜0
组卷：14引用：2难度：0.7
解析
6．已知f（x）是定义在R上的增函数，且对任意x∈R，都有f（x₁）f（x₂）=f（x₁+x₂），则不等式
f
（
x
-
2
）
＞
[
f
（
x
+
1
2
）
]
2
的解集为（　　）
A．（-3，+∞） B．（2，+∞） C．（-∞，-3） D．（-∞，2）
组卷：42引用：3难度：0.5
解析
7．若函数y=
lo
g
1
3
（
a
x
2
-
4
x
+
12
）
在区间[1，2]上单调递增，则实数a的取值范围（　　）
A．（-1，1] B．[-1，1] C．（0，1] D．[0，1]
组卷：239引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.

21．已知定义在R上的增函数f（x），函数F（x）=f（x）-f（-x），G（x）=f（x）+f（-x）．
（1）用定义证明函数F（x）是增函数，并判断其奇偶性；
（2）若f（x）=2^x，不等式G（2x）+4＞mG（x）对任意x∈R恒成立，求实数m的取值范围；
（3）在（2）的条件下，函数g（x）=F（x）+a（f（1-x）-a）有两个不同的零点x₁，x₂，且1+x₁x₂＜x₁+x₂，求实数a的取值范围．
组卷：21引用：3难度：0.4
解析
22．设定义在实数集R上的函数f（x）（恒不为0），若存在不等于1的正常数k,对于任意实数x,等式f（k+x）=k²f（x）恒成立，则称函数y=f（x）为P（k）函数．
（Ⅰ）若函数f（x）=2^x为P（k）函数，求出k的值；
（Ⅱ）设
1
＜
a
＜
e
2
e
，其中e为自然对数的底数，函数g（x）=a^x．
①比较
g
（
2
lna
）
与a^e的大小；
②判断函数g（x）=a^x是否为P（k）函数，若是，请证明；若不是，试说明理由．
组卷：45引用：5难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．6.32×10¹⁴¹s	B．6.32×10¹⁴⁰s
C．3.16×10¹⁴¹s	D．3.16×10¹⁴⁰s

A．a＞1，m＞0，b＜0	B．a＞1，m＜0，b＞0
C．0＜a＜1，m＜0，b＞0	D．0＜a＜1，m＜0，b＜0

2022-2023学年河南省信阳高级中学高一（上）月考数学试卷（1月份）（一）

一、单选题（本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．下列函数中，其定义域和值域分别与函数y=elnx的定义域和值域相同的是（ ）

2．已知ab=-5，则a-ba+b-ab的值是（ ）

4．已知a=sin53°，b=log52，c=0.50.8，则a,b,c的大小关系为（ ）

5．已知函数f（x）=loga|x+m|2x2+b的图象如图所示，当x＜n时，有f（x）＞0，则下列判断中正确的是（ ）

6．已知f（x）是定义在R上的增函数，且对任意x∈R，都有f（x1）f（x2）=f（x1+x2），则不等式f（x-2）＞[f（x+12）]2的解集为（ ）

7．若函数y=log13（ax2-4x+12）在区间[1，2]上单调递增，则实数a的取值范围（ ）

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤.

1．下列函数中，其定义域和值域分别与函数y=e^lnx的定义域和值域相同的是（　　）

2．已知ab=-5，则
a
-
b
a
+
b
-
a
b
的值是（　　）

4．已知a=sin53°，b=log₅2，c=0.5^0.8，则a,b,c的大小关系为（　　）

5．已知函数
f
（
x
）
=
lo
g
a
|
x
+
m
|
2
x
2
+
b
的图象如图所示，当x＜n时，有f（x）＞0，则下列判断中正确的是（　　）

6．已知f（x）是定义在R上的增函数，且对任意x∈R，都有f（x₁）f（x₂）=f（x₁+x₂），则不等式
f
（
x
-
2
）
＞
[
f
（
x
+
1
2
）
]
2
的解集为（　　）

7．若函数y=
lo
g
1
3
（
a
x
2
-
4
x
+
12
）
在区间[1，2]上单调递增，则实数a的取值范围（　　）