2022-2023学年四川省成都市十县市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知

  sinα

  =

  -

  1

  2

  ，则cos2α=（　　）

  A． 3 2

  B． - 3 2

  C． 1 2

  D． - 1 2
  组卷：234引用：1难度：0.9

  解析

• 2．已知

  a

  ，

  b

  为共线向量，且

  a

  =

  （

  2

  ，

  x

  ）

  （

  x

  ∈

  R

  ）

  ，

  b

  =

  （

  1

  ，

  3

  ）

  ，则

  |

  a

  |

  =（　　）

  A． 2 10

  B． 3 10

  C．40

  D． 3 5
  组卷：146引用：1难度：0.9

  解析

• 3．已知i为虚数单位，复数z的共轭复数为

  z

  ，且满足zi=3+2i,则

  z

  +

  z

  =（　　）

  A．-4

  B．0

  C．4

  D．6i
  组卷：28引用：1难度：0.7

  解析

• 4．l,m是不同的直线，α，β，y是互不相同的平面，下列说法正确的是（　　）

  A．若直线l,m在平面α内，且均平行平面β，则平面α与平面β平行

  B．若平面α平行直线l,直线l平行平面γ，则平面α与平面γ平行

  C．若平面α垂直平面γ，平面β垂直平面γ，则平面α与平面β平行

  D．若直线l垂直平面α，直线m垂直平面α，则直线l与直线m平行
  组卷：31引用：1难度：0.6

  解析

• 5．在△ABC中，AB=1，

  BC

  =

  2

  ，

  AC

  =

  3

  ，则

  BC

  •

  CA

  的值为（　　）

  A．2

  B．-2

  C． 2 3

  D． - 2 3
  组卷：52引用：1难度：0.7

  解析

• 6．已知a,b,c分别为△ABC三个内角A，B，C的对边，且满足a+b=（cosA+cosB）c,则△ABC为（　　）

  A．锐角三角形	B．直角三角形
  C．钝角三角形	D．以上皆有可能
  组卷：29引用：1难度：0.7

  解析

• 7．“辛普森（Simpson）公式”给出了求几何体体积的一种估算方法：几何体的体积V等于其上底面的面积S、中截面（过高的中点且平行于底面的截面）的面积S₁的4倍、下底面S₂之和乘以高h的六分之一，即

  V

  =

  1

  6

  h

  （

  S

  +

  4

  S

  1

  +

  S

  2

  ）

  ．我们把所有顶点都在两个平行平面内的多面体称为拟柱体，在这两个平行平面内的面叫作拟柱体的底面，其余各面叫作拟柱体的侧面，中国古代名词“刍童”（原来是草堆的意思）就是指上下底面皆为矩形的拟柱体，已知某个“刍童”如图所示，AB=2，AD=1，EF=3，EH=2，且体积为

  46

  3

  ，则它的高为（　　）

  A． 53 12

  B． 53 15

  C．4

  D．3
  组卷：42引用：1难度：0.7

  解析

四、解答题：本题共6.小题，共70分。解答应写出文字说明、证明过程或演算步骤。

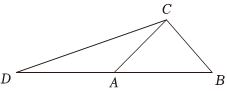• 21．世界大学生夏季运动会，素有“小奥运会”之称，由国际大学生体育联合会（InternationalUniversitySportsFederation）主办，只限在校大学生和毕业不超过两年的．大学生（年龄限制为17～28岁）参加的世界大型综合性运动会．始办于1959年，其前身为国际大学生运动会．第31届世界大学生夏季运动会即将在成都拉开帷幕，为了配合大运会的基础设施建设，组委会拟在成都东安湖公园一角修建具有成都文化特色的观景步道（如图）．在△BCD中，

  ∠

  BDC

  =

  π

  6

  ，A是BD边上一点，AD=20米，

  ∠

  ACB

  =

  π

  2

  ．
  （1）若

  AC

  =

  10

  2

  米，求BC；
  （2）当AD≥AC，记∠ACD=θ，求当角θ取何值时，△ACD的面积最大，并求出这个最大值，
  组卷：30引用：1难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  3

  sinxcosx

  +

  1

  2

  （

  si

  n

  4

  x

  -

  co

  s

  4

  x

  ）

  -

  1

  （

  x

  ∈

  R

  ）

  ，函数y=f（x）的图象向左平移

  π

  6

  个单位，再向上平移1个单位得到y=g（x）的图象，h（x）=-cosx|cosx-3m|+m（m∈R）．
  （1）若f（α）=0，求α；
  （2）若对任意

  x

  2

  ∈

  [

  -

  π

  2

  ，

  π

  6

  ]

  ，存在

  x

  1

  ∈

  [

  0

  ，

  π

  2

  ]

  使得g（x₁）=h（x₂）成立，求实数m的取值范围．
  组卷：124引用：1难度：0.3

  解析