当前位置：试卷中心 > 试卷详情

2022-2023学年宁夏石嘴山三中高三（上）期中数学试卷（理科）

发布：2024/8/31 8:0:8

1．下列六个关系式：①0∈{0}，②∅∈{0}，③∅⊆{0}，④∅={0}，⑤A⊆A，⑥A∩A=∅；其中正确的个数为（　　）
A．5个 B．4个 C．3个 D．2个
组卷：59引用：2难度：0.7
解析
2．定积分
∫
3
π
2
0
sinxdx=（　　）
A．2 B．1 C．0 D．-1
组卷：87引用：3难度：0.9
解析
3．在△ABC中，已知sin²A+2sin²B=sin²C，则该三角形的形状为（　　）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形
组卷：286引用：4难度：0.6
解析
4．已知点A（0，1），B（2，3），向量
BC
=（-3，1），则向量
AC
=（　　）
A．（1，-2） B．（-1，2） C．（1，-3） D．（-1，3）
组卷：434引用：6难度：0.8
解析
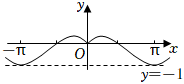5．函数f（x）的部分图象如图所示，则f（x）的解析式可能为（　　）
A．f（x）=
3
xsinx
1
+
2
x
2
B．f（x）=
x
2
sinx
1
+
x
2
C．f（x）=
3
x
2
cosx
1
+
2
x
2
D．f（x）=
x
2
cosx
1
+
x
2
组卷：231引用：7难度：0.8
解析
6．若m,n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题错误的是（　　）
A．若α∥β，β∥γ，则α∥γ B．若m∥n,α∥β，n⊥α，则m⊥β
C．若m⊥α，α⊥β，则m∥β D．若m⊥α，m⊥β，则α∥β
组卷：52引用：3难度：0.8
解析
7．函数f（x）=sinx（sinx+cosx）的最小正周期是（　　）
A．
π
3
B．
π
2
C．π D．2π
组卷：174引用：3难度：0.8
解析

21．已知数列{a_n}，a₁=1，S_n为数列{a_n}的前n项和，且S_n=
1
3
（n+2）a_n．
（1）求数列{a_n}的通项公式；
（2）求证：sina_n-a_n＜0；
（3）证明：（1+sin
1
a
1
）（1+sin
1
a
2
）（1+sin
1
a
3
）…（1+sin
1
a
n
）＜e²．
组卷：392引用：6难度：0.2
解析
22．已知函数f（x）=|x-1|+2|x+1|．
（Ⅰ）求不等式f（x）＜5的解集；
（Ⅱ）设f（x）的最小值为m.若正实数a,b,c满足a+2b+3c=m,求3a²+2b²+c²的最小值．
组卷：43引用：3难度：0.5
解析

A．f（x）= 3 xsinx 1 + 2 x 2	B．f（x）= x 2 sinx 1 + x 2
C．f（x）= 3 x 2 cosx 1 + 2 x 2	D．f（x）= x 2 cosx 1 + x 2

A．若α∥β，β∥γ，则α∥γ	B．若m∥n,α∥β，n⊥α，则m⊥β
C．若m⊥α，α⊥β，则m∥β	D．若m⊥α，m⊥β，则α∥β

1．下列六个关系式：①0∈{0}，②∅∈{0}，③∅⊆{0}，④∅={0}，⑤A⊆A，⑥A∩A=∅；其中正确的个数为（ ）