2023-2024学年湖北省襄阳五中高二（上）起点数学试卷

一、选择题：本题共8小题，每小题5分，共40.0分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合P={x|x²-x-2≤0}，Q={x|log₂（x-1）≤1}，则（∁_RP）∩Q等于（　　）

  A．[2，3]	B．（-∞，-1]∪[3，+∞）
  C．（2，3]	D．（-∞，-1]∪（3，+∞）
  组卷：135引用：12难度：0.9

  解析

• 2．已知不重合的平面α、β、γ和直线l,则“α∥β”的充分不必要条件是（　　）

  A．α内有无数条直线与β平行

  B．α内的任何直线都与β平行

  C．α⊥γ且γ⊥β

  D．l⊥α且l⊥β
  组卷：35引用：7难度：0.7

  解析

• 3．如果函数y=x²+（1-a）x+2在区间（4，+∞）上单调递增．那么实数a的取值范围是（　　）

  A．（-∞，9]

  B．（-∞，-3]

  C．[5，+∞）

  D．（-∞，-7]
  组卷：161引用：7难度：0.7

  解析

• 4．在△ABC中，a=6，

  b

  =

  6

  3

  ，A=30°，则最长边c=（　　）

  A．6

  B．12

  C．6或12

  D． 6 3
  组卷：131引用：5难度：0.6

  解析

• 5．已知向量

  a

  =（2，-3，1），

  b

  =（2，0，3），

  c

  =（0，0，2），则

  a

  •（

  b

  +

  c

  ）=（　　）

  A．8

  B．9

  C．13

  D． 61
  组卷：215引用：9难度：0.9

  解析

• 6．二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=2，AC=3，BD=4，

  CD

  =

  41

  ，则该二面角的大小为（　　）

  A．30°

  B．120°

  C．60°

  D．45°
  组卷：151引用：9难度：0.5

  解析

• 7．四面体ABCD的四个顶点都在球O的球面上，AB=BC=CD=DA=4，

  AC

  =

  BD

  =

  2

  2

  ，点E，F，G分别为棱BC，CD，AD的中点，现有如下结论：
  ①过点E，F，G作四面体ABCD的截面，则该截面的面积为2；
  ②四面体ABCD的体积为

  16

  3

  3

  ；
  ③过E作球O的截面，则截面面积的最大值与最小值的比为5：4．
  则上述说法正确的个数是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：42引用：4难度：0.5

  解析

四、解答题：本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤.

• 21．已知向量

  m

  =

  （

  2

  sinθ

  ，

  sinθ

  -

  cosθ

  ）

  ，

  n

  =

  （

  cosθ

  ，-

  2

  -

  m

  ）

  ，函数

  f

  （

  θ

  ）

  =

  m

  •

  n

  的最小值为g（m）．
  （1）求g（m）；
  （2）函数h（x）为定义在R上的增函数，且对任意的x₁，x₂都满足h（x₁+x₂）=h（x₁）+h（x₂），问：是否存在这样的实数m,使不等式

  h

  （

  4

  sinθ

  -

  cosθ

  ）

  +

  h

  （

  2

  m

  +

  3

  ）

  ＞

  h

  （

  f

  （

  θ

  ）

  ）

  对所有

  θ

  ∈

  （

  π

  4

  ，

  π

  ）

  恒成立，若存在，求出m的取值范围；若不存在，说明理由．
  组卷：53引用：7难度：0.3

  解析

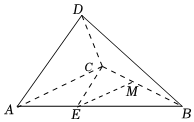• 22．如图，在三棱锥D-ABC中，

  AD

  =

  CD

  =

  AE

  =

  CE

  =

  1

  2

  BC

  ，CD⊥AD，记二面角D-AC-B的平面角为θ．
  （1）若

  θ

  =

  π

  3

  ，BC=2，求三棱锥D-ABC的体积；
  （2）若M为BC的中点，求直线AD与EM所成角的取值范围．
  组卷：204引用：5难度：0.4

  解析