2022-2023学年河北省石家庄市高二(下)期末数学试卷
发布:2024/5/29 8:0:9
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.某物体做直线运动,其运动规律是
,则它在第4秒末的瞬时速度为( )s=t2+3t组卷:81引用:4难度:0.9 -
2.
的展开式中含x2的项的系数为( )(1+1x)(1+x)4组卷:234引用:5难度:0.9 -
3.函数y=
x2-lnx的单调递减区间为( )12组卷:3620引用:129难度:0.9 -
4.甲乙两人进行乒乓球决赛,比赛采取七局四胜制.现在的情形是甲胜3局,乙胜2局.若两人胜每局的概率相同,则甲获得冠军的概率为( )
组卷:93引用:4难度:0.7 -
5.曲线y=xe1-x在点(1,1)处的切线方程为( )
组卷:38引用:1难度:0.7 -
6.为落实立德树人的根本任务,践行五育并举,某学校开设A,B,C三门德育校本课程,现有甲、乙、丙、丁、戊五位同学参加校本课程的学习,每位同学仅报一门,每门至少有一位同学参加,则不同的报名方法有( )
组卷:284引用:7难度:0.7 -
7.我们将服从二项分布的随机变量称为二项随机变量,服从正态分布的随机变量称为正态随机变量.概率论中有一个重要的结论是棣莫弗一拉普拉斯极限定理,它表明,若随机变量Y~B(n,p),当n充分大时,二项随机变量Y可以由正态随机变量X来近似,且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同.棣莫弗在1733年证明了
的特殊情形,1812年,拉普拉斯对一般的p进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数超过60次的概率为( )p=12
(附:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.6827,P(μ-2σ≤X≤μ+2σ)≈0.9545,P(μ-3σ≤X≤μ+3σ)≈0.9973)组卷:369引用:11难度:0.8
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
-
21.近年来,明代著名医药学家李时珍故乡黄冈市蕲春县大力发展大健康产业,蕲艾产业化种植已经成为该县脱贫攻坚的主要产业之一,已知蕲艾的株高y(单位:cm)与一定范围内的温度x(单位:℃)有关,现收集了蕲艾的13组观测数据,得到如下的散点图:
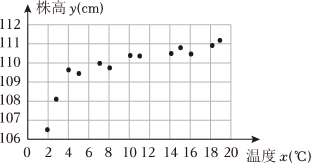
现根据散点图利用或y=a+bx建立y关于x的经验回归方程,令y=c+dx,s=x得到如下数据:t=1x
设(si,yi)与(ti,yi)(i=1,2,3…13)的相关系数分别为r1,r2,且r2=-0.9953.xyst13∑i=1siyi-13s•y10.15 109.94 3.04 0.16 13.94 13∑i=1tiyi-13t•y13∑i=1s2i-13s213∑i=1t2i-13t213∑i=1y2i-13y2-2.1 11.67 0.21 21.22
(Ⅰ)用相关系数说明用哪种模型建立y与x的经验回归方程更合适;
(Ⅱ)根据(Ⅰ)的结果及表中数据,建立y关于x的经验回归方程;
(Ⅲ)已知蕲艾的利润z(万元)与x、y的关系为,当x为何值时,z的预测值最大.z=20y-12x
参考数据和公式:0.21×21.22=4.4562,11.67×21.22=247.6374,,对于一组数据(ui,vi)(i=1,2,3,…,n),其回归直线方程247.6374=15.7365的斜率和截距的最小二乘法估计分别为̂v=̂βu+̂α,̂β=n∑i=1uivi-nu•vn∑i=1u2i-nu2,相关系数̂α=v-̂βu.r=n∑i=1uivi-nu•vn∑i=1u2i-nu2•n∑i=1v2i-nu2组卷:32引用:1难度:0.7 -
22.已知函数f(x)=lnx+ax2+(2a+1)x.
(1)讨论f(x)的单调性;
(2)当a<0时,证明:.f(x)≤-34a-2组卷:2747引用:38难度:0.5


