2022-2023学年福建省厦门市集美区蔡林学校八年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题4分，共40分）

• 1．自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1312引用：50难度：0.9

  解析

• 2．已知三角形的两边长分别为2、10，则第三边长可能是（　　）

  A．6

  B．8

  C．10

  D．12
  组卷：132引用：5难度：0.6

  解析

• 3．四边形的内角和为（　　）

  A．180°

  B．360°

  C．540°

  D．720°
  组卷：252引用：29难度：0.9

  解析

• 4．点P（-1，-2）关于y轴对称的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：77引用：3难度：0.8

  解析

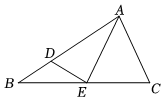• 5．如图，在△ABC中，点D，E分别是边AB，BC上的点，连接AE和DE，则下列是△BDE的外角的是（　　）

  A．∠AED

  B．∠AEC

  C．∠ADE

  D．∠BAE
  组卷：314引用：8难度：0.7

  解析

• 6．整式n²-1与n²+n的公因式是（　　）

  A．n

  B．n2

  C．n+1

  D．n-1
  组卷：149引用：5难度：0.8

  解析

• 7．若等腰三角形中有一个角等于80°，则这个等腰三角形的顶角的度数为（　　）

  A．100°

  B．80°

  C．80°或20°

  D．50°或80°
  组卷：133引用：8难度：0.8

  解析

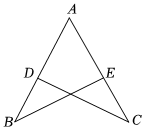• 8．已知：如图，D、E分别在AB、AC上，若AB=AC，AD=AE，∠A=60°，∠B=35°，则∠ADC的度数是（　　）

  A．95°

  B．90°

  C．85°

  D．80°
  组卷：16引用：4难度：0.5

  解析

三、解答题（本题有9小题，共82分）

• 24．规定两数a,b之间的一种运算，记作（a,b）：如果a^c=b,那么（a,b）=c.
  例如：因为2³=8，所以（2，8）=3．
  （1）根据上述规定，填空：（5，25）=

  ，（-2，4）=

  ，（-3，81）=

  ；
  （2）小明在研究这种运算时发现一个现象：（3ⁿ，4ⁿ）=（3，4），他给出了如下的证明：
  设（3ⁿ，4ⁿ）=x,则（3ⁿ）^x=4ⁿ，即（3^x）ⁿ=4ⁿ．
  ∴3^x=4，即（3，4）=x,
  ∴（3ⁿ，4ⁿ）=（3，4）．
  请你尝试运用上述这种方法说明下面这个等式成立的理由．（4，7）+（4，8）=（4，56）．
  组卷：269引用：5难度：0.5

  解析

• 25．如图，在△ABC中，∠ABC=90°，AB=BC，点A，B分别在坐标轴上．
  （1）如图1，若点C的横坐标为-3，点B的坐标为

  ；
  （2）如图2，若x轴恰好平分∠BAC，BC交x轴于点M，过C点作CD垂直x轴于D点，试猜想线段CD与AM的数量关系，并说明理由；
  （3）如图3，OB=BF，∠OBF=90°，连接CF交y轴于点P，点B在y轴正半轴上运动时，△BPC与△AOB的面积比是否变化？若不变，求其值，若变化，求其取值范围．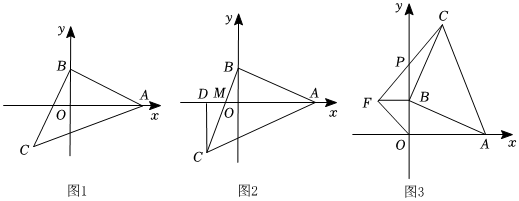
  
  组卷：273引用：4难度：0.2

  解析