2022-2023学年安徽省滁州市定远县育才学校高二（上）期末数学试卷

一、选择题（本大题共8小题，共40分．在每小题列出的选项中，选出符合题目的一项）

• 1．下列命题正确的是（　　）

  A．若 a 与 b 共线， b 与 c 共线，则 a 与 c 共线

  B．向量 a ， b ， c 共面，即它们所在的直线共面

  C．若 a ∥ b ，则存在唯一的实数λ，使 a =λ b

  D．零向量是模为0，方向任意的向量
  组卷：211引用：1难度：0.8

  解析

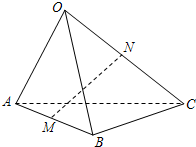• 2．已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，用

  a

  ，

  b

  ，

  c

  表示

  MN

  ，则

  MN

  等于（　　）

  A． 1 2 （ b + c - a ）

  B． 1 2 （ a + b - c ）

  C． 1 2 （ a - b + c ）

  D． 1 2 （ c - a - b ）
  组卷：2922引用：41难度：0.9

  解析

• 3．已知空间向量

  a

  =（m+1，m,-2），

  b

  =（-2，1，4），且

  a

  ⊥

  b

  ，则m的值为（　　）

  A．- 10 3

  B．-10

  C．10

  D． 10 3
  组卷：191引用：16难度：0.7

  解析

• 4．已知A（2，4），B（1，0），动点P在直线x=-1上，当|PA|+|PB|取最小值时，则点P的坐标为（　　）

  A． （ - 1 ， 8 5 ）

  B． （ - 1 ， 21 5 ）

  C．（-1，2）

  D．（-1，1）
  组卷：481引用：7难度：0.7

  解析

• 5．直线l过圆C：x²+y²-6y+5=0的圆心，并且与直线x+y+2=0垂直，则直线l的方程为（　　）

  A．x+y-2=0

  B．x-y+2=0

  C．x+y-3=0

  D．x-y+3=0
  组卷：4引用：4难度：0.8

  解析

• 6．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的右焦点为F，过点F作圆x²+y²=b²的切线，若两条切线互相垂直，则椭圆C的离心率为（　　）

  A． 1 2

  B． 2 2

  C． 2 3

  D． 6 3
  组卷：1015引用：16难度：0.6

  解析

• 7．动点M分别与两定点A（-5，0），B（5，0）连线的斜率的乘积为

  -

  16

  25

  ，设点M的轨迹为曲线C，已知N（2，

  3

  ），F（-3，0），则|MF|+|MN|的最小值为（　　）

  A．4

  B．8

  C．2 3

  D．12
  组卷：112引用：3难度：0.6

  解析

四、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）

• 21．已知椭圆的焦点在x轴上，且过点

  （

  3

  2

  ，

  3

  ）

  ，焦距为

  2

  5

  ，设P为椭圆上的一点，F₁、F₂是该椭圆的两个焦点，若∠F₁PF₂=60°，求：
  （1）椭圆的标准方程；
  （2）△PF₁F₂的面积．
  组卷：294引用：5难度：0.5

  解析

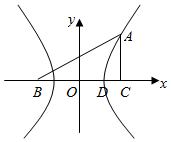• 22．如图平面直角坐标系xOy中，直角三角形ABC，∠C=90°，B，C在x轴上且关于原点O对称，D在边BC上，

  1

  3

  BD=DC，△ABC的周长为12．若双曲线E以B，C为焦点，且经过A，D两点．
  （1）求双曲线E的渐近线方程；
  （2）若一过点P（m,0）（m为非零常数）的直线与双曲线E相交于不同于双曲线顶点的两点M，N，且

  MP

  =

  λ

  PN

  ，问在x轴上是否存在定点G，使

  BC

  ⊥

  （

  GM

  -

  λ

  GN

  ）

  ？若存在，求出所有这样定点G的坐标；若不存在，请说明理由．
  组卷：170引用：2难度：0.4

  解析