2022-2023学年广东省深圳市南山实验教育集团华侨城高级中学高一（上）期中数学试卷

一、选择题（共8小题，每小题5分。每小题只有一个选项符合题意）

• 1．设集合A={x∈N|x²-x-2＜0}，则集合A的真子集有（　　）

  A．3个

  B．4个

  C．5个

  D．6个
  组卷：424引用：4难度：0.9

  解析

• 2．函数y=

  2

  x

  -

  3

  +

  1

  x

  -

  3

  的定义域为（　　）

  A．[ 3 2 ，+∞）	B．（-∞，3）∪（3，+∞）
  C．[ 3 2 ，3）∪（3，+∞）	D．（3，+∞）
  组卷：2983引用：33难度：0.9

  解析

• 3．关于x的不等式2^x-3＜8的解集为（　　）

  A．（-∞，6）

  B．（3，+∞）

  C．（6，+∞）

  D．（-∞，3）
  组卷：39引用：2难度：0.7

  解析

• 4．设a∈R，则“a＞1”是“a²＞a”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：7831引用：112难度：0.7

  解析

• 5．若函数

  y

  =

  （

  2

  +

  x

  ）

  （

  m

  -

  x

  ）

  为偶函数，则m=（　　）

  A．-2

  B．2

  C． - 2

  D． 2
  组卷：466引用：2难度：0.9

  解析

• 6．设a=0.6^0.4，b=0.4^0.6，c=0.4^0.4，则a,b,c的大小关系是（　　）

  A．c＞a＞b

  B．a＞b＞c

  C．a＞c＞b

  D．b＞c＞a
  组卷：259引用：4难度：0.9

  解析

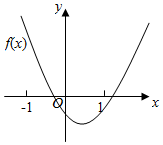• 7．已知函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=a^x+b的图象是（　　）

  A．

  B．

  C．

  D．
  组卷：1300引用：213难度：0.9

  解析

四、解答题（共6小题，共70分）

• 21．已知函数

  f

  （

  x

  ）

  =

  ax

  +

  b

  x

  2

  +

  4

  是定义在（-2，2）上的奇函数，且

  f

  （

  1

  2

  ）

  =

  2

  17

  ．
  （1）求函数f（x）的解析式；
  （2）证明：函数f（x）在区间（-2，2）上单调递增；
  （3）若f（a+1）+f（1-2a）＞0，求实数a的取值范围．
  组卷：234引用：7难度：0.5

  解析

• 22．设函数y=f（x）（x∈R），当x＞0时，f（x）＞1，且对任意实数x₁，x₂满足f（x₁+x₂）=f（x₁）•f（x₂），当x₁≠x₂时，f（x₁）≠f（x₂）．
  （1）求证：函数y=f（x）在R上为单调递增函数；
  （2）当x₁≠x₂时，试比较

  1

  2

  [

  f

  （

  x

  1

  ）

  +

  f

  （

  x

  2

  ）

  ]

  与

  f

  （

  x

  1

  +

  x

  2

  2

  ）

  的大小．
  组卷：177引用：2难度：0.4

  解析