2022-2023学年新疆昌吉州高中学联体高二（下）期末数学试卷

一、单选题（本题共8小题每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．设集合M={x∈R|0≤x≤2}，N={x∈N|-1＜x＜3}，则M∩N=（　　）

  A．{1，2}

  B．{0，1，2}

  C．{x|0≤x≤2}

  D．{x|-1＜x＜3}
  组卷：241引用：7难度：0.9

  解析

• 2．“sinθ＜0”是“θ为第三象限角”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：17引用：1难度：0.7

  解析

• 3．已知（1-i）z=4+2i（i为虚数单位），则|z|=（　　）

  A． 10

  B．10

  C． 5

  D．5
  组卷：6引用：1难度：0.8

  解析

• 4．下列函数中，既是偶函数又在（0，+∞）上是减函数的是（　　）

  A．f（x）=x3

  B．f（x）=0.3x

  C．f（x）=lg|x|

  D． f （ x ） = 1 x 2
  组卷：44引用：1难度：0.8

  解析

• 5．（1+2x）⁶的二项展开式中含x³项的系数为（　　）

  A．240

  B．16

  C．160

  D．60
  组卷：42引用：2难度：0.8

  解析

• 6．材料：已知三角形三边长分别为a,b,c,则三角形的面积为

  S

  =

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ，其中

  p

  =

  a

  +

  b

  +

  c

  2

  ，这个公式被称为海伦—秦九韶公式．根据材料解答：已知△ABC中，BC=2，AB+AC=4，则△ABC面积的最大值为（　　）

  A． 4 3

  B． 2 3

  C．3

  D． 3
  组卷：25引用：2难度：0.7

  解析

• 7．已知角θ的顶点与原点重合，始边与x轴非负半轴重合，终边过点（1，2），则sin2θ=（　　）

  A． - 4 5

  B． - 3 5

  C． 3 5

  D． 4 5
  组卷：28引用：2难度：0.7

  解析

四、解答题（本题共70分，第17题10分，18—22题每题12分．解答应写出文字说明、证明过程或验算步骤）

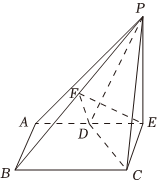• 21．如图，四棱锥P-ABCD的底面ABCD是梯形，AD∥BC，AB⊥BC，E为AD延长线上一点，PE⊥平面ABCD，PE=2AD，tan∠PDE=2，F是PB中点．
  （1）证明：EF⊥PA；
  （2）若BC=2AD=2，三棱锥E-PDC的体积为

  1

  3

  ，求锐二面角F-DC-B的余弦值．
  组卷：33引用：1难度：0.5

  解析

• 22．某商场举行有奖促销活动，凡7月7日当天消费每超过400元（含400元），均可抽奖一次，抽奖箱里有6个形状、大小、质地完全相同的小球，其中红球有3个，白球有3个，抽奖方案设置两种，顾客自行选择其中的一种方案．
  方案一：从抽奖箱中，一次性摸出2个球，若摸出2个红球，则打6折；若摸出1个红球，则打8折；若没摸出红球，则不打折；
  方案二：从抽奖箱中，有放回地每次摸取1个球，连摸2次，每摸到1次红球，立减80元．
  （1）若小方、小红均分别消费了400元，且均选择抽奖方案一，试求他们其中恰有一人享受6折优惠的概率；
  （2）若小勇消费恰好满500元，试比较说明小勇选择哪种方案更划算．
  组卷：18引用：2难度：0.5

  解析