2022-2023学年山西省大同市八年级(上)期中数学试卷
发布:2024/8/30 6:0:10
一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
-
1.-8的立方根是( )
组卷:1634引用:37难度:0.7 -
2.面积为5的正方形的边长是( )
组卷:410引用:3难度:0.5 -
3.下列计算结果正确的是( )
组卷:21引用:2难度:0.8 -
 4.公元前3世纪,古希腊数学家欧几里得编写了《几何原本》.他在编写这本书时挑选一部分数学名词和公认的真命题(即公理)作为证实其他命题的出发点和依据,除公理外,其他命题的真假都需要通过演绎推理的方法进行判断.在此基础上,逐渐形成了一种重要的数学思想.这种思想是( )组卷:318引用:7难度:0.6
4.公元前3世纪,古希腊数学家欧几里得编写了《几何原本》.他在编写这本书时挑选一部分数学名词和公认的真命题(即公理)作为证实其他命题的出发点和依据,除公理外,其他命题的真假都需要通过演绎推理的方法进行判断.在此基础上,逐渐形成了一种重要的数学思想.这种思想是( )组卷:318引用:7难度:0.6 -
5.下列代数式变形中,属于因式分解的是( )
组卷:176引用:4难度:0.7 -
6.下列命题中,是真命题的是( )
组卷:213引用:3难度:0.7 -
7.按如图所示的程序计算,若开始输入的值为25,则最后输出的y值是( )
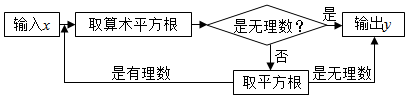 组卷:591引用:6难度:0.7
组卷:591引用:6难度:0.7
三、解答题(本大题含8个小题,共72分.解答应写出必要的文字说明、证明过程或演算步骤.)
-
22.数学小组的同学们探究
的近似值,探究过程如下:137
解:∵112=121,122=144,
∴,11<137<12
∵设,其中0<x<1,137=11+x
∴137=(11+x)2,即137=121+22x+x2,
∵x2较小省略,
∴121+22x≈137,
∴x≈0.72,
∴137≈11.72
问题:
(1)填空:的小数部分的近似值约为 (结果保留两位小数).76
(2)请参照数学小组求近似值的探究过程,写出求137近似值的探究过程.233组卷:12引用:2难度:0.5 -
23.【实践操作】
(1)如图①,在边长为a的大正方形中剪去一个边长为b的小正方形(a>b),把图①中L形的纸片按图②剪拼,改造成了一个大长方形如图③,请求出图③中大长方形的面积;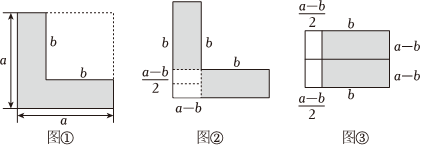
(2)请写出图①、图②、图③验证的乘法公式为:.
【应用探究】
(3)利用(2)中验证的公式简便计算:499×501+1;
(4)计算:.(1-122)×(1-132)×(1-142)×…×(1-120212)×(1-120222)
【知识迁移】
(5)类似地,我们还可以通过对立体图形进行变换得到代数恒等式如图④,将一个棱长为a的正方体中去掉一个棱长为b的正方体,再把剩余立体图形切割分成三部分如图⑤,利用立体图形的体积,可得恒等式为:a3-b3=.(结果不需要化简)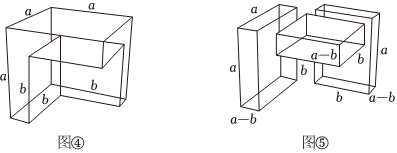 组卷:83引用:2难度:0.5
组卷:83引用:2难度:0.5


