2021-2022学年江西省南昌市育山高级中学高一（下）期中数学试卷

一、单选题（本题共12小题，每题5分，共60分）

• 1．已知角α的终边过点P（4，m）（m≠0），且

  sinα

  =

  m

  5

  ，则cosα的值为（　　）

  A．± 3 5

  B． - 3 5

  C．± 4 5

  D． 4 5
  组卷：601引用：5难度：0.7

  解析

• 2．函数

  y

  =

  cos

  （

  2

  x

  +

  π

  3

  ）

  的图象（　　）

  A．关于点（ π 3 ，0）对称	B．关于点（ π 6 ，0）对称
  C．关于直线 x = π 6 对称	D．关于直线 x = π 3 对称
  组卷：611引用：5难度：0.9

  解析

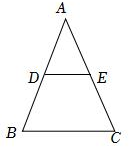• 3．如图，在△ABC中，AB=AC，D，E分别是AB，AC的中点，则（　　）

  A． AB 与 AC 共线

  B． DE 与 CB 共线

  C． CD 与 AE 相等

  D． AD 与 BD 相等
  组卷：376引用：3难度：0.7

  解析

• 4．已知sinα、cosα是方程5x²-

  5

  x-2=0的两个实根，且α∈（0，π），则cos（α+

  π

  4

  ）=（　　）

  A． 10 10

  B．- 10 10

  C． 3 10 10

  D．- 3 10 10
  组卷：307引用：4难度：0.7

  解析

• 5．已知扇形OAB的圆心角为4rad,面积为8，则该扇形的周长为（　　）

  A．12

  B．10

  C． 8 2

  D． 4 2
  组卷：230引用：2难度：0.8

  解析

• 6．把函数y=f（x）图像上所有点的横坐标缩短到原来的

  1

  2

  倍，纵坐标不变，再把所得曲线向右平移

  π

  3

  个单位长度，得到函数y=sin（x-

  π

  4

  ）的图像，则f（x）=（　　）

  A．sin（ x 2 - 7 π 12 ）	B．sin（ x 2 + π 12 ）
  C．sin（2x- 7 π 12 ）	D．sin（2x+ π 12 ）
  组卷：8342引用：38难度：0.8

  解析

• 7．已知

  PA

  =

  -

  4

  7

  AB

  ，设

  BP

  =

  λ

  PA

  ，则λ=（　　）

  A． 4 3

  B． - 4 3

  C． - 3 4

  D． 3 4
  组卷：10引用：1难度：0.8

  解析

三、解答题（本题共6题，共70分）

• 21．已知函数f（x）=cos

  x

  4

  sin

  x

  4

  +

  cos

  2

  x

  4

  ．
  （Ⅰ）求函数f（x）的最小正周期和单调递增区间；
  （Ⅱ）若x∈[0，2π]，求函数f（x）的值域．
  组卷：200引用：2难度：0.6

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  2

  sin

  ωx

  2

  cos

  （

  ωx

  2

  -

  π

  3

  ）

  +

  m

  （

  ω

  ＞

  0

  ）

  ．在下列条件①、条件②、条件③这三个条件中，选择可以确定ω和m值的两个条件作为已知．
  （1）求

  f

  （

  π

  4

  ）

  的值；
  （2）若函数f（x）在区间[0，a]上是增函数，求实数a的最大值．
  条件①：f（x）的最小正周期为π；
  条件②：f（x）的最大值与最小值之和为0；
  条件③：f（0）=2．
  组卷：190引用：4难度：0.5

  解析