2022-2023学年吉林省四平第一高级中学高三（上）期初数学试卷

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x||x|≤3}，B={x|2-x＞0}，则A∩B=（　　）

  A．{0}

  B．{0，-1，-2，1}

  C．（2，3]

  D．[-3，2）
  组卷：39引用：7难度：0.8

  解析

• 2．2（1-i）²+（1+i）²=（　　）

  A．-2

  B．2

  C．-2i

  D．2i
  组卷：32引用：6难度：0.8

  解析

• 3．已知向量

  a

  =（1，-2），

  b

  =（m,3-m），若

  a

  ⊥

  b

  ，则m=（　　）

  A．-3

  B．2

  C．1

  D．-2
  组卷：94引用：7难度：0.8

  解析

• 4．一封闭的正方体容器ABCD-A₁B₁C₁D₁，P，Q，R分别是AB，BC和C₁D₁的中点，由于某种原因，P，Q，R处各有一个小洞，当此容器内存水的表面恰好经过这三个小洞时，容器中水的上表面形状是（　　）

  A．三角形

  B．四边形

  C．五边形

  D．六边形
  组卷：60引用：9难度：0.7

  解析

• 5．若关于x的不等式ax²-（a²+6a+9）x+a+1＜0的解集是（x|m＜x＜n），则

  1

  m

  +

  1

  n

  的最小值为（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：414引用：6难度：0.6

  解析

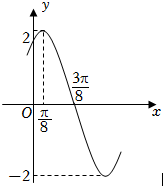• 6．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

  π

  2

  ）的部分图象如图所示，将函数f（x）的图象向右平移

  3

  π

  16

  个单位长度，再将图象上所有点的横坐标变为原来的2倍（纵坐标不变），得到函数y=g（x）的图象，则g（x）=（　　）

  A．2sin（x- π 8 ）	B．2sin（x+ π 8 ）
  C．2sin（4x- π 8 ）	D．2sin（4x+ π 8 ）
  组卷：277引用：8难度：0.5

  解析

• 7．“方程

  x

  2

  m

  +

  2

  +

  y

  2

  2

  -

  m

  =

  1

  表示椭圆”的一个充分条件是（　　）

  A．-2＜m＜0

  B．m=0

  C．m＜-2

  D．m＞0
  组卷：754引用：3难度：0.8

  解析

三、解答题（本大题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤）

• 21．已知函数f（x）=

  a

  x

  -x+alnx存在两个极值点x₁，x₂．
  （1）求a的取值范围；
  （2）求f（x₁）+f（x₂）-3a的最小值．
  组卷：280引用：11难度：0.6

  解析

• 22．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的一条渐近线方程为y=

  13

  x,一个焦点到该渐近线的距离为

  39

  ．
  （1）求C的方程；
  （2）设A，B是直线x=-9上关于x轴对称的两点，直线y=k（x+9）与C交于M，N两点，证明：直线AM与BN的交点在定直线上．
  组卷：111引用：4难度：0.5

  解析