2022-2023学年湖北省云学新高考联盟学校高一（下）联考数学试卷（5月份）

一、单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知全集U=A∪B={x∈N|0＜x+1＜6}，A={1，2}，若A∩B=∅，则B=（　　）

  A．{0，3，4}

  B．{0，1}

  C．{-1，0}

  D．{2，3，4}
  组卷：92引用：2难度：0.7

  解析

• 2．已知复数

  z

  =

  2

  +

  ai

  1

  +

  2

  i

  （其中i是虚数单位）是实数，则实数a的值是（　　）

  A．-1

  B．2

  C．3

  D．4
  组卷：47引用：3难度：0.8

  解析

• 3．△ABC中内角A，B，C所对的边分别是a,b,c,（a+b+c）（a+c-b）=3ac,sinB=2sinAcosC，那么△ABC是（　　）

  A．等边三角形	B．等腰三角形
  C．直角三角形	D．等腰直角三角形
  组卷：35引用：4难度：0.8

  解析

• 4．函数

  f

  （

  x

  ）

  =

  2

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  的最小正周期为π，将f（x）的图象向右平移

  π

  6

  个单位长度后，得到一个偶函数的图象，则（　　）

  A． φ = π 3

  B． φ = π 6

  C． φ = - π 3

  D． φ = - π 6
  组卷：197引用：3难度：0.8

  解析

• 5．△ABC的斜二测画法的直观图为△A′B′C′，A′B′=4，B′C′=3，

  ∠

  A

  ′

  B

  ′

  C

  ′

  =

  π

  6

  ，则△ABC的面积为（　　）

  A．3

  B． 6 2

  C． 6 6

  D． 12 6
  组卷：63引用：2难度：0.8

  解析

• 6．△ABC中内角A，B，C所对的边分别是a,b,c,若△ABC的面积为

  a

  2

  +

  b

  2

  -

  c

  2

  4

  ，则tanC=（　　）

  A． 2 2

  B． 3 3

  C．1

  D． 3
  组卷：76引用：2难度：0.7

  解析

• 7．在△ABC中，AB=AC=2，

  BC

  =

  2

  3

  ，D为BC的中点，将△ACD绕AD旋转至APD，使得

  BP

  =

  6

  ，则三棱锥P-ABD的外接球表面积为（　　）

  A． 8 2 π 3

  B． 5 5 π 6

  C．7π

  D．8π
  组卷：52引用：2难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

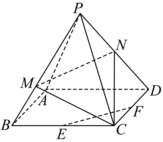• 21．如图，在正四棱锥P-ABCD中AB=2，PA=4，

  PM

  =

  2

  MB

  ，N、E、F分别为PD、BC、CD中点．
  （1）求证：EF∥平面PMN；
  （2）三棱锥N-MCD的体积．
  组卷：70引用：3难度：0.5

  解析

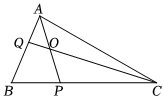• 22．已知△ABC中，AB=2，AC=3，

  BP

  =

  1

  3

  BC

  ，Q是边AB（含端点）上的动点．
  （1）若

  AQ

  =

  2

  5

  AB

  ，O点为AP与CQ的交点，请用

  AB

  ，

  AC

  表示

  AO

  ；
  （2）若点Q使得

  AP

  ⊥

  CO

  ，求cos∠BAC的取值范围及S_△AQC的最大值．
  组卷：64引用：2难度：0.4

  解析