2022-2023学年河南省南阳市高一(下)期中数学试卷
发布:2024/5/16 8:0:9
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1.sin
的值是( )14π3组卷:174引用:4难度:0.9 -
2.在△ABC中,内角A,B,C的对边分别为a,b,c,且A=30°,a=3,b=4,则满足条件的三角形有( )
组卷:124引用:2难度:0.8 -
3.若α为第三象限角且
,则sin(π-α)=-35=( )cos(π2-α)组卷:238引用:1难度:0.8 -
4.下列说法正确的是( )
组卷:65引用:2难度:0.8 -
5.将函数y=cos(3x+φ)的图象沿x轴向左平移
个单位后,得到的函数的图象关于原点对称,则φ的一个可能值为( )π12组卷:159引用:4难度:0.7 -
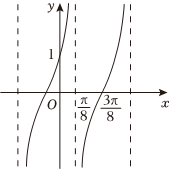 6.已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<),y=f(x)的部分图象如图,则π2=( )f(7π24)组卷:118引用:1难度:0.8
6.已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<),y=f(x)的部分图象如图,则π2=( )f(7π24)组卷:118引用:1难度:0.8 -
7.在△ABC中,AC=BC=1,∠C=900.P为AB边上的动点,则
的取值范围是( )PB•PC组卷:998引用:6难度:0.6
四、解答题(本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
-
21.已知△ABC的内角A,B,C所对的边分别为a,b,c.向量
,e=(b,c),f=(sinC,sinB).g=(c-a,b-a)
(1)若,求证:△ABC为等腰三角形;e∥f
(2)若,a=2,e⊥g求△ABC的面积.A=π3组卷:57引用:3难度:0.5 -
22.已知函数f(x)=2cos(ωx+φ)+
(0<ω<2,0<φ<2).请在下面的三个条件中任选两个解答问题.①函数f(x)的图象过点(0,2π2);②函数f(x)的图象关于点(2)对称;③函数f(x)相邻两个对称轴之间距离为2.12,2
(1)求函数f(x)的解析式;
(2)当a∈(-2,0)时,是否存在实数a满足不等式f(2a+)>f(a)?若存在,求出a的范围,若不存在,请说明理由.32组卷:48引用:3难度:0.4


