当前位置：试卷中心 > 试卷详情

2021-2022学年新疆喀什地区疏附县职业高中高二（上）月考数学试卷（12月份）

发布：2024/6/10 8:0:9

一、单选题（本题共16小题，每小题2分，共32分）

1．抛物线y=
1
4
x
2
的焦点坐标是（　　）
A．（
1
16
，0） B．
（
-
1
16
，
0
）
C．（0，1） D．（1，0）
组卷：2引用：2难度：0.9
解析
2．已知椭圆
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，F₁，F₂分别为椭圆的左、右焦点，若椭圆上存在一点P，使得|PF₁|-|PF₂|=2b,则该椭圆离心率的取值范围为（　　）
A．
（
0
，
1
2
]
B．
[
1
2
，
1
）
C．
（
0
，
2
2
]
D．
[
2
2
，
1
）
组卷：2引用：1难度：0.7
解析
3．若点P为抛物线y=2x²上的动点，F为抛物线的焦点，则|PF|的最小值为（　　）
A．2 B．
1
2
C．
1
4
D．
1
8
组卷：21引用：2难度：0.8
解析
4．已知抛物线y=px²（其中p为常数）经过点A（1，3），则抛物线的焦点到准线的距离等于（　　）
A．
9
2
B．
3
2
C．
1
18
D．
1
6
组卷：1引用：1难度：0.8
解析
5．长轴长为8，以抛物线
y
=
1
12
x
2
的焦点为一个焦点的椭圆的标准方程为（　　）
A．
x
2
55
+
y
2
64
=
1
B．
x
2
28
+
y
2
64
=
1
C．
x
2
16
+
y
2
25
=
1
D．
x
2
7
+
y
2
16
=
1
组卷：2引用：1难度：0.8
解析
6．抛物线x²=
1
a
y的准线方程是y-2=0，则a的值是（　　）
A．
1
8
B．-
1
8
C．8 D．-8
组卷：7引用：1难度：0.8
解析
7．如果椭圆
x
2
100
+
y
2
36
=1上一点P到焦点F₁的距离为6，则点P到另一个焦点F₂的距离为（　　）
A．10 B．6 C．12 D．14
组卷：25引用：2难度：0.5
解析
8．在平面直角坐标系中，经过点P（2
2
，-
2
），渐近线方程为y=
±
2
x的双曲线的标准方程为（　　）
A．
x
2
4
-
y
2
2
=
1
B．
x
2
7
-
y
2
14
=
1
C．
x
2
3
-
y
2
6
=
1
D．
y
2
14
-
x
2
7
=
1
组卷：6引用：1难度：0.8
解析
9．已知直线l经过点O（0，0），且点A（0，4），B（2，0）到l的距离相等，则l被经过O，A，B三点的圆所截得的弦长为（　　）
A．
6
5
5
或2
5
B．
3
5
5
C．
3
5
5
或2
5
D．2
5
组卷：2引用：1难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共4小题，每小题9分，共36分）

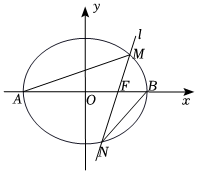27．如图，已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
过点（1，
3
2
），离心率为
1
2
，A，B分别是椭圆C的左，右顶点，过右焦点F且斜率为k（k＞0）的直线l与椭圆相交于M，N两点．
（1）求椭圆C的标准方程；
（2）记△AFM，△BFN的面积分别为S₁，S₂，若
S
1
S
2
=
6
5
，求k的值；
（3）记直线AM、BN的斜率分别为k₁，k₂，求
k
2
k
1
的值．
组卷：9引用：1难度：0.3
解析
28．已知中心在坐标原点O，焦点在x轴上，离心率为
3
2
的椭圆C过点
（
3
，
1
2
）
．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）是否存在不过原点O的直线l：y=kx+m与C交于PQ两点，使得OP、PQ、OQ的斜率依次成等比数列．若存在，求出k、m满足条件；若不存在，请说明理由．
组卷：4引用：1难度：0.6
解析