2022-2023学年湖北省武汉市华中师大一附中高二(上)月考数学试卷(12月份)
发布:2024/8/11 10:0:1
一、选择题(共8小题,每小题5分,满分40分)
-
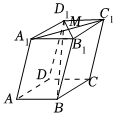 1.如图,在平行六面体ABCD-A1B1C1D1中,M是A1C1与B1D1的交点,若,AB=a,AD=b,且AA1=c,则x+y+z等于( )MB=xa+yb+zc组卷:69引用:4难度:0.7
1.如图,在平行六面体ABCD-A1B1C1D1中,M是A1C1与B1D1的交点,若,AB=a,AD=b,且AA1=c,则x+y+z等于( )MB=xa+yb+zc组卷:69引用:4难度:0.7 -
2.已知向量
共面,则实数t的值是( )a=(-2,1,3),b=(-1,3,2),c=(1,t,-1)组卷:426引用:6难度:0.7 -
3.已知△ABC的三个顶点分别为A(5,3,2),B(1,-1,3),C(-1,-3,5),则BC边上的中线长为( )
组卷:173引用:4难度:0.8 -
4.已知椭圆C:
+y2=1的左、右焦点分别为F1,F2,过F2的直线l交椭圆C于A,B两点,若△ABF1内切圆的周长为x22,则直线l的方程为( )45π9组卷:299引用:5难度:0.2 -
5.已知抛物线C:y2=2px(p>0)的焦点为F,点M在抛物线C的准线l上,线段MF与y轴交于点A,与抛物线C交于点B,若|AB|=1,|MA|=3,则p=( )
组卷:148引用:5难度:0.6 -
6.已知F为抛物线y2=x的焦点,点A,B,C在抛物线上,F为△ABC的重心,则|AF|+|BF|+|CF|=( )
组卷:423引用:7难度:0.5 -
7.已知直线l:x+y-4=0上动点P,过点P向圆x2+y2=1引切线,则切线长的最小值是( )
组卷:238引用:7难度:0.6
四、解答题(共6小题,满分70分)
-
21.已知椭圆C的方程为
=1(a>b>0),右焦点为F(x2a2+y2b2,0),且离心率为2.63
(1)求椭圆C的方程;
(2)设M,N是椭圆C上的两点,直线MN与曲线x2+y2=b2(x>0)相切.证明:M,N,F三点共线的充要条件是|MN|=.3组卷:449引用:8难度:0.6 -
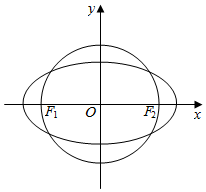 22.如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(-3,12,0),F2(3,0),圆O的直径为F1F2.3
22.如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(-3,12,0),F2(3,0),圆O的直径为F1F2.3
(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.267组卷:5424引用:12难度:0.5


