2022-2023学年江西省吉安市青原区双校联盟高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．已知z=

  （

  1

  +

  3

  i

  ）

  （

  3

  -

  i

  ）

  2

  3

  -

  4

  i

  ，则

  z

  •

  z

  =（　　）

  A．1

  B．2

  C．4

  D．16
  组卷：48引用：4难度：0.8

  解析

• 2．如图，一个平面图形的斜二测画法的直观图是一个边长为a的正方形，则原平面图形的面积为（　　）
  

  A． 2 4 a2

  B．a2

  C．2 2 a2

  D．2a2
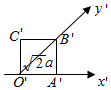  组卷：529引用：14难度：0.9

  解析

• 3．记cos（-80°）=k,那么tan280°=（　　）

  A． 1 - k 2 k

  B． - 1 - k 2 k

  C． k 1 - k 2

  D． - k 1 - k 2
  组卷：992引用：8难度：0.7

  解析

• 4．已知tanθ=2，则

  sin

  （

  π

  2

  +

  θ

  ）

  -

  cos

  （

  π

  -

  θ

  ）

  sin

  （

  π

  2

  -

  θ

  ）

  -

  sin

  （

  π

  -

  θ

  ）

  =（　　）

  A．2

  B．-2

  C．0

  D． 2 3
  组卷：1450引用：31难度：0.7

  解析

• 5．下列说法不正确的是（　　）

  A．若棱柱被一平面所截，则分成的两部分不一定是棱柱

  B．当球心到平面的距离小于球面半径时，球面与平面的交线总是一个圆

  C．平行于圆台底面的平面截圆台，截面是圆面

  D．直角三角形绕它的一边旋转一周形成的曲面围成的几何体是圆锥
  组卷：32引用：3难度：0.7

  解析

• 6．直线y=3与函数f（x）=tanωx（ω＞0）的图象的交点中，相邻两点的距离为

  π

  4

  ，则

  f

  （

  π

  12

  ）

  =（　　）

  A． - 3

  B． - 3 3

  C． 3 3

  D． 3
  组卷：21引用：2难度：0.7

  解析

• 7．将函数

  f

  （

  x

  ）

  =

  cos

  （

  π

  3

  -

  2

  x

  ）

  -

  2

  sin

  （

  π

  4

  +

  x

  ）

  sin

  （

  π

  4

  -

  x

  ）

  的图象左移

  π

  12

  ，得到函数y=g（x）的图象，则y=g（x）在

  [

  -

  π

  12

  ，

  π

  2

  ]

  上对应的单调递增区间是（　　）

  A． [ - π 6 ， π ]

  B． [ - π 6 ， π 2 ]

  C． [ - π 12 ， π 2 ]

  D． [ - π 12 ， π 4 ]
  组卷：99引用：2难度：0.5

  解析

四、解答题（共70分）

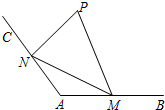• 21．如图，洪泽湖湿地为拓展旅游业务，现准备在湿地内建造一个观景台P，已知射线AB，AC为湿地两边夹角为120°的公路（长度均超过2千米），在两条公路AB，AC上分别设立游客接送点M，N，从观景台P到M，N建造两条观光线路PM，PN，测得AM=2千米，AN=2千米．
  （1）求线段MN的长度；
  （2）若∠MPN=60°，求两条观光线路PM与PN之和的最大值．
  组卷：747引用：17难度：0.3

  解析

• 22．如图①梯形ABCD中AD∥BC，AB=

  3

  ，BC=1，

  CD

  =

  2

  ，BE⊥AD且BE=1，将梯形沿BE折叠得到图②，使平面ABE⊥平面BCDE，CE与BD相交于O，点P在AB上，且AP=2PB，R是CD的中点，过O，P，R三点的平面交AC于Q．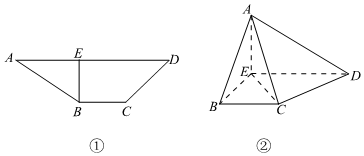
  
  （1）证明：Q是AC的中点；
  （2）证明：AD⊥平面BEQ；
  （3）M是AB上一点，已知二面角M-EC-B为45°，求

  AM

  AB

  的值．
  组卷：286引用：8难度：0.5

  解析