当前位置：试卷中心 > 试卷详情

2023年江苏省常州市武进区前黄实验学校中考数学适应性试卷

发布：2024/6/15 8:0:9

一.选择题（本大题共8小题，每小题2分，共16分.在每小题所给出的四个选项中，只有一项是正确的）

1．-2的相反数是（　　）
A．2 B．-2 C．
1
2
D．
-
1
2
组卷：1193引用：63难度：0.9
解析
2．计算（-a³）²的结果是（　　）
A．-a⁵ B．a⁵ C．-a⁶ D．a⁶
组卷：2979引用：122难度：0.9
解析
3．几何体中主视图为圆的是（　　）
A． B． C． D．
组卷：46引用：2难度：0.9
解析
4．若a＞b,则下列四个选项中一定成立的是（　　）
A．a²＞b² B．-3a＞-3b C．
a
4
＜
b
4
D．a+2＞b+2
组卷：341引用：3难度：0.8
解析
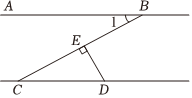5．如图，直线AB∥CD，DE⊥BC于点E，若∠CDE=57°，则∠1的度数是（　　）
A．57° B．33° C．23° D．47°
组卷：72引用：4难度：0.6
解析
6．如图，将左边的四边形的两边延长后，形成△PAB，显然△PAB的周长比原四边形的周长大，能正确解释这一现象的数学知识是（　　）
A．两点确定一条直线
B．两直线相交只有一个交点
C．垂线段最短
D．两点之间，线段最短
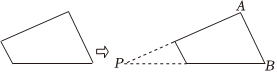组卷：333引用：4难度：0.8
解析
7．如图，⊙O中，CD是切线，切点是D，直线CO交⊙O于B、A，∠A=20°，则∠C的度数是（　　）
A．25° B．65° C．50° D．75°
组卷：1884引用：17难度：0.7
解析
8．若一张圆形纸片能裁剪出一个三边长分别为13，14，15的三角形，则此圆形纸片的半径最小是（　　）
A．8 B．
65
8
C．
65
4
D．
33
4
组卷：214引用：2难度：0.9
解析

二.填空题（本大题共10小题，每小题2分，共20分.请将正确答案写在答题卡相对应的位置）

9．化简：
4
=
．
组卷：133引用：4难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（本大题共10小题，共84分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤等.）

27．概念引入
定义：平面直角坐标系中，若点P（x,y）满足：|x|+|y|=4，则点P叫做“复兴点”．例如：图①中的P（1，3）是“复兴点”
概念理解
（1）在点A（2，2），B（
3
2
，-
5
2
），C（-1，5）中，是“复兴点”的点为
；
初步探究
（2）如图②，在平面直角坐标系中，画出所有“复兴点”的集合．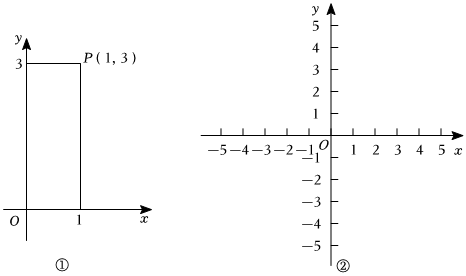

深入探究
（3）若反比例函数y=
k
x
（k≠0）的图象上存在4个“复兴点”，则k的取值范围是
．
（4）若一次函数y=kx-2k+3（k≠0）的图象上存在“复兴点”，直接写出“复兴点”的个数及对应的k的取值范围．
组卷：673引用：4难度：0.4
解析
28．【定义】若抛物线与一水平直线交于两点，我们把这两点间线段的长称为抛物线关于这条直线的跨径，抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高，矢高与跨径的比值称为抛物线关于这条直线的矢跨比．
如图1，抛物线y=ax²+bx+c的顶点为P，PC⊥x轴于点C，它与x轴交于点A，B，则AB的长为抛物线y=ax²+bx+c关于x轴的跨径，PC的长为抛物线y=ax²+bx+c关于x轴的矢高，
PC
AB
的值为抛物线y=ax²+bx+c关于x轴的矢跨比．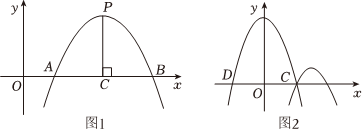

【特例】如图2，已知抛物线y=-x²+4与x轴交于点C，D（点C在点D右侧）；
①抛物线y=-x²+4关于x轴的矢高是
，跨径是
，矢跨比是
；
②有一抛物线经过点C，与抛物线y=-x²+4开口方向与大小一样，且矢高是抛物线y=-x²+4关于x轴的矢高的
1
4
，求它关于x轴的矢跨比；
【推广】结合抛物线的平移规律可以发现，两条开口方向与大小一样的抛物线，若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k（k＞0）倍，则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的
倍（用含k的代数式表示）；
【应用】如图3是某地一座三拱桥梁建筑示意图，其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线，它们关于水平钢梁所在直线的跨径分别为420米与280米，已知主跨的矢跨比为
1
6
，则边跨的矢跨比是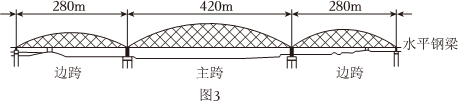
．
组卷：1219引用：3难度：0.4
解析