当前位置：试卷中心 > 试卷详情

2022-2023学年黑龙江省佳木斯市富锦一中高二（下）第一次月考数学试卷

发布：2024/7/12 8:0:9

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1．已知直线l₁经过A（3，7），B（2，8）两点，且直线l₂⊥l₁，则直线l₂的倾斜角为（　　）
A．30° B．45° C．135° D．150°
组卷：104引用：3难度：0.7
解析
2．已知函数f（x）=alnx+x²的图象在x=1处的切线方程为3x-y+b=0，则a+b=（　　）
A．-2 B．-1 C．0 D．1
组卷：375引用：10难度：0.7
解析
3．下列导数运算正确的是（　　）
A．（x+
1
x
）′=1+
1
x
2
B．（2^x）′=x2^x-1
C．（cosx）′=sinx D．（xlnx）′=lnx+1
组卷：671引用：3难度：0.7
解析
4．定义在区间
[
-
1
2
，
4
]
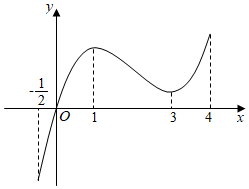上的函数f（x）的导函数f'（x）的图象如图所示，则下列结论正确的是（　　）
A．函数f（x）在区间（1，4）上单调递增
B．函数f（x）在区间（1，3）上单调递减
C．函数f（x）在x=1处取得极大值
D．函数f（x）在x=0处取得极大值
组卷：581引用：8难度：0.7
解析
5．已知A（4，9），B（6，3）两点，以线段AB为直径的圆的标准方程是（　　）
A．（x+5）²+（y+6）²=10 B．（x+5）²+（y+6）²=20
C．（x-5）²+（y-6）²=20 D．（x-5）²+（y-6）²=10
组卷：86引用：5难度：0.7
解析
6．已知椭圆C：
x
2
m
+
y
2
m
+
6
=1的离心率为
3
2
，则C的长轴长为（　　）
A．8
2
B．4
2
C．2
2
D．4
组卷：752引用：9难度：0.7
解析
7．如图，已知双曲线C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦点分别为F₁，F₂，以OF₂为直径的圆与双曲线C的渐近线在第一象限的交点为P，线段PF₁与另一条渐近线交于点Q，且△OPF₂的面积是△OPQ面积的2倍，则该双曲线的渐近线方程为（　　）
A．
y
=±
2
2
x
B．
y
=±
14
2
x
C．y=±x D．
y
=±
2
x
组卷：72引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：（本大题共6小题，共计70分）

21．已知函数f（x）=lnx-ax²+x,a∈R．
（1）当a=0时，求曲线y=f（x）在点（e,f（e））处的切线方程；
（2）讨论f（x）的单调性．
组卷：20引用：2难度：0.5
解析
22．已知椭圆Γ：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的左焦点为F（-1，0），左、右顶点及上顶点分别记为A、B、C，且
CF
•
CB
=1．
（1）求椭圆Γ的方程；
（2）设过F的直线PQ交椭圆Γ于P、Q两点，若直线PA、QA与直线l：x+4=0分别交于M、N两点，l与x轴的交点为K，则|MK|•|KN|是否为定值？若为定值，请求出该定值；若不为定值，请说明理由．
组卷：327引用：3难度：0.6
解析