2022-2023学年新疆乌鲁木齐七十中高一（下）学情调研数学试卷

一、选择题（本大题共8小题，每小题5分，共40分）在每小题所给出的四个选项中，只有一项是符合题目要求的.

• 1．设复数z满足z=i（i-2），（i为虚数单位），则复数z在复平面内所对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：18引用：2难度：0.8

  解析

• 2．下列命题正确的是（　　）

  A．若 a • b = a • c ，则 b = c

  B．若| a + b |=| a - b |，则 a • b =0

  C．若 a ∥ b ， b ∥ c ，则 a ∥ c

  D．若 a 与 b 是单位向量，则 a • b =1
  组卷：145引用：16难度：0.9

  解析

• 3．已知a,b为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（　　）

  A．若a∥b,b∥α，则a∥α	B．若a∥b,a⊥α，b∥β，则α⊥β
  C．若a∥α，b∥β，α∥β，则a∥b	D．若a∥α，b∥β，α⊥β，则a⊥b
  组卷：118引用：4难度：0.7

  解析

• 4．在△ABC中，若

  a

  =

  5

  3

  b

  ,

  A

  =

  2

  B

  ，则cosB等于（　　）

  A． 5 3

  B． 5 4

  C． 5 5

  D． 5 6
  组卷：62引用：2难度：0.7

  解析

• 5．菱形ABCD在平面α内，PC⊥α，则PA与BD的位置关系是（　　）

  A．平行	B．相交但不垂直
  C．垂直相交	D．异面且垂直
  组卷：188引用：9难度：0.9

  解析

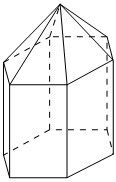• 6．为了给热爱朗读的师生提供一个安静独立的环境，乌鲁木齐市70中学修建了若干“朗读亭”．如图，该朗读亭的外形是一个正六棱柱和正六棱锥的组合体，正六棱柱两条相对侧棱所在的轴截面为正方形，若正六棱锥的高与底面边长的比为3：4，则正六棱锥与正六棱柱的侧面积的比值为（　　）

  A． 7 8

  B． 21 16

  C． 43 16

  D． 43 24
  组卷：40引用：2难度：0.5

  解析

• 7．已知

  AB

  ⊥

  AC

  ，

  3

  |

  AB

  |

  =

  2

  |

  AC

  |

  =

  6

  m

  （m＞0），若点M是△ABC所在平面内的一点，且

  AM

  =

  AB

  |

  AB

  |

  -

  m

  AC

  |

  AC

  |

  ，则

  MB

  •

  MC

  的最小值为（　　）

  A． 1 6

  B． 1 4

  C． 3 4

  D． 5 6
  组卷：26引用：2难度：0.6

  解析

四、解答题（本大题共6小题，第17题满分70分，其余各题满分70分共70分.请在答题卡指定区域作答，解答时应写出文字说明、证明过程或演算步骤.）

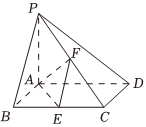• 21．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，PA⊥平面ABCD，∠ABC=60°，E为BC的中点，F为边PC上的一个点．
  （1）求证：平面AEF⊥平面PAD；
  （2）若H为PD上的动点，EH与平面PAD所成角的正切值的最大值为

  6

  2

  ，求平面PAB与平面PCD夹角的余弦值．
  组卷：69引用：2难度：0.5

  解析

• 22．定义函数f（x）=asinx+bcosx的“伴随向量”为

  OM

  =

  （

  a

  ,

  b

  ）

  ，向量

  OM

  =

  （

  a

  ,

  b

  ）

  的“伴随函数”为f（x）=asinx+bcosx.
  （1）写出函数

  g

  （

  x

  ）

  =

  cos

  （

  x

  +

  π

  6

  ）

  -

  sinx

  的“伴随向量”

  OM

  ，并求

  |

  OM

  |

  ；
  （2）记向量

  OM

  =

  （

  1

  ，

  3

  ）

  的伴随函数为φ（x），若当

  x

  ∈

  [

  0

  ，

  π

  2

  ）

  时，不等式

  φ

  （

  x

  ）

  +

  kφ

  （

  x

  +

  π

  3

  ）

  ＞

  0

  恒成立，求实数k的取值范围．
  组卷：17引用：2难度：0.5

  解析