2022-2023学年甘肃省白银市靖远二中高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．设集合A={x|-1≤x＜3}，B={1，2，3，4}，则A∩B=（　　）

  A．{1}

  B．{1，2}

  C．{2，3}

  D．{1，2，3}
  组卷：303引用：7难度：0.8

  解析

• 2．已知复数z=2+i,且

  az

  -

  z

  +

  b

  =

  0

  ，其中a,b为实数，则（　　）

  A．a=-1，b=-4

  B．a=-1，b=4

  C．a=1，b=-4

  D．a=1，b=4
  组卷：77引用：5难度：0.8

  解析

• 3．坐标轴与圆C：x²+y²-4x-2y+1=0的交点个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：165引用：4难度：0.6

  解析

• 4．函数

  f

  （

  x

  ）

  =

  e

  x

  x

  的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：33引用：5难度：0.7

  解析

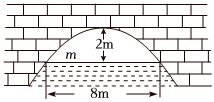• 5．如图中是抛物线形拱桥，当水面在m时，拱顶距离水面2米，水面宽度为8米，则当水面宽度为10米时，拱顶与水面之间的距离为（　　）

  A． 25 2 米

  B． 25 4 米

  C． 25 6 米

  D． 25 8 米
  组卷：58引用：4难度：0.6

  解析

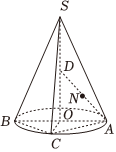• 6．如图，在圆锥SO中，AB是底面圆O的直径，SO=AB=4，AC=DC，D为OS的中点，N为AD的中点，则点N到平面SBC的距离为（　　）

  A． 4 3

  B． 5 3

  C．1

  D．2
  组卷：48引用：4难度：0.5

  解析

• 7．某市场供应的黄瓜中，来自甲地的占40%，来自乙地的占30%，来自丙地的占30%，甲地、乙地供应的黄瓜的新鲜率（按斤计算）均为95%，丙地供应的黄瓜的新鲜率（按斤计算）是p.从该市场供应的黄瓜中任意购买一斤，若这斤黄瓜新鲜的概率为93.5%，则p=（　　）

  A．85%

  B．88%

  C．90%

  D．92%
  组卷：132引用：1难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知函数f（x）=alnx+ax+1．
  （1）当a=1时，求f（x）的图像在点（1，f（1））处的切线方程；
  （2）若不等式f（x）≤xe^x恒成立，求a的取值集合．
  组卷：139引用：5难度：0.4

  解析

• 22．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）经过点P（4，2），双曲线C的右焦点F到其渐近线的距离为2．
  （1）求双曲线C的方程；
  （2）已知Q（0，-2），D为PQ的中点，作PQ的平行线l与双曲线C交于不同的两点A，B，直线AQ与双曲线C交于另一点M，直线BQ与双曲线C交于另一点N，证明：M，N，D三点共线．
  组卷：177引用：5难度：0.3

  解析