2022-2023学年浙江省丽水市缙云中学等四校高一（上）联考数学试卷（12月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点（-2，1），则sinα的值为（　　）

  A． - 5 5

  B． 5 5

  C． - 2 5 5

  D． 2 5 5
  组卷：12引用：4难度：0.8

  解析

• 2．已知全集U=R，集合

  A

  =

  {

  x

  |

  |

  x

  -

  1

  |

  ≤

  3

  }

  ，

  B

  =

  {

  x

  |

  x

  -

  5

  x

  +

  1

  ＜

  0

  }

  ，那么A∪B=（　　）

  A．（-1，4）

  B．（-1，4]

  C．（-2，5）

  D．[-2，5）
  组卷：18引用：3难度：0.7

  解析

• 3．下面命题中不正确的是（　　）

  A．“a＞1”是“ 1 a ＜ 1 ”的充分不必要条件

  B．命题“∀x∈R，x2+x+1＜0”的否定是“∃x∈R，x2+x+1≥0

  C．设x,y∈R，若“x+y≥4”则“x≥2且y≥2”是真命题

  D．设a,b∈R，则“a≠0且b≠0”是“ab≠0”的充要条件
  组卷：184引用：4难度：0.8

  解析

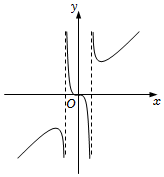• 4．函数f（x）的部分图象如图所示，则f（x）的解析式可能是（　　）

  A． f （ x ） = x 3 1 - | x |	B． f （ x ） = x x 2 + 1
  C． f （ x ） = x 3 x 2 - 1	D． f （ x ） = x 2 + 1 x 2 - 1
  组卷：231引用：8难度：0.7

  解析

• 5．已知a=sin

  5

  π

  6

  ，b=ln2，c=2 ^0.3，则a,b,c的大小关系为（　　）

  A．a＜b＜c

  B．c＜b＜a

  C．b＜a＜c

  D．a＜c＜b
  组卷：30引用：4难度：0.9

  解析

• 6．已知f（x）是定义在R上的增函数，且对任意x∈R，都有f（x₁）f（x₂）=f（x₁+x₂），则不等式

  f

  （

  x

  -

  2

  ）

  ＞

  [

  f

  （

  x

  +

  1

  2

  ）

  ]

  2

  的解集为（　　）

  A．（-3，+∞）

  B．（2，+∞）

  C．（-∞，-3）

  D．（-∞，2）
  组卷：42引用：3难度：0.5

  解析

• 7．若函数y=

  lo

  g

  1

  3

  （

  a

  x

  2

  -

  4

  x

  +

  12

  ）

  在区间[1，2]上单调递增，则实数a的取值范围（　　）

  A．（-1，1]

  B．[-1，1]

  C．（0，1]

  D．[0，1]
  组卷：239引用：5难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤

• 21．已知

  f

  （

  lo

  g

  2

  x

  ）

  =

  x

  -

  1

  x

  ．
  （1）求函数f（x）的表达式，并判断函数f（x）的单调性（不需要证明）；
  （2）关于x的不等式4^1+x+4^1-x-8+3f（x）≥kf²（x）在[1，+∞）上有解，求实数k的取值范围．
  组卷：180引用：3难度：0.6

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  |

  3

  x

  2

  -

  ax

  |

  +

  x

  2

  -

  x

  +

  1

  （

  x

  ＞

  0

  ）

  ，

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  x

  ．
  （1）若a=1，求f（x）的值域；
  （2）对任意x₀∈[3，4]，存在

  x

  1

  ，

  x

  2

  ∈

  [

  1

  8

  ，

  2

  ]

  （

  x

  1

  ≠

  x

  2

  ）

  ，使得x₀=g（x₁）=g（x₂），求实数a的取值范围．
  组卷：27引用：3难度：0.4

  解析