2023-2024学年天津二十中高三（上）期中数学试卷

一、单选题（本大题共10小题，共50分.在每小题列出的选项中，选出符合题目的一项）

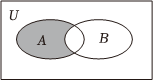• 1．已知全集U=R，集合A={0，1，2，3，4，5，6}，B={x|

  x

  3

  -

  x

  ≤0}，则图中阴影部分表示的集合为（　　）

  A．{1，2}

  B．{0，1，2}

  C．{1，2，3}

  D．{0，1，2，3}
  组卷：246引用：4难度：0.8

  解析

• 2．设a,b是平面α内两条不同的直线，l是平面α外的一条直线，则“l⊥a,l⊥b”是“l⊥α”的（　　）

  A．充要条件

  B．充分而不必要的条件

  C．必要而不充分的条件

  D．既不充分也不必要的条件
  组卷：152引用：52难度：0.9

  解析

• 3．函数y=

  sin

  2

  x

  1

  +

  cosx

  的部分图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：119引用：8难度：0.7

  解析

• 4．已知a=log_1.40.7，b=1.4^0.7，c=0.7^1.4，则a,b,c的大小关系是（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．c＜a＜b

  D．c＜b＜a
  组卷：295引用：4难度：0.8

  解析

• 5．《莱茵德纸草书》（RhindPapyrus）是世界上最古老的数学著作之一，书中有这样一道题目：把93个面包分给5个人，使每个人所得面包个数成等比数列，且使较小的两份面包个数之和等于中间一份面包个数的四分之三，则中间一份面包的个数为（　　）

  A．8

  B．12

  C．16

  D．20
  组卷：179引用：4难度：0.8

  解析

• 6．已知

  sin

  （

  x

  +

  π

  12

  ）

  =

  -

  1

  4

  ，则

  cos

  （

  5

  π

  6

  -

  2

  x

  ）

  =（　　）

  A． 7 8

  B． 1 8

  C． - 7 8

  D． - 1 8
  组卷：293引用：4难度：0.5

  解析

• 7．将函数

  f

  （

  x

  ）

  =

  2

  sinxcosx

  +

  3

  cos

  2

  x

  的图象向右平移

  π

  3

  个单位，得到g（x）的图象，再将g（x）图象上的所有点的横坐标变成原来的

  1

  2

  ，得到h（x）的图象，则下列说法正确的个数是（　　）
  ①函数h（x）的最小正周期为2π；
  ②

  （

  π

  3

  ，

  0

  ）

  是函数h（x）图象的一个对称中心；
  ③函数h（x）图象的一个对称轴方程为

  x

  =

  5

  π

  6

  ；
  ④函数h（x）在区间

  [

  -

  π

  24

  ，

  5

  π

  24

  ]

  上单调递增

  A．1

  B．2

  C．3

  D．4
  组卷：970引用：7难度：0.5

  解析

三、解答题（本大题共4小题，共60分.解答应写出文字说明，证明过程或演算步骤）

• 21．已知等差数列{a_n}的前n项和为S_n，a₁=1，S₄=10，数列{b_n}满足：b₁=3，

  b

  n

  +

  1

  =

  2

  b

  n

  -

  1

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）证明：{b_n-1}是等比数列；
  （2）证明：S_2n+1•b_n＞2S_n•b_n+1；
  （3）设数列{c_n}满足：

  c

  n

  =

  a n + 1 a 2 n a 2 n + 2 ， n 为奇数

  a 2 n b n ， n 为偶数

  ．证明：

  2

  n

  ∑

  k

  =

  1

  c

  k

  ＜

  9

  4

  ．
  组卷：710引用：4难度：0.4

  解析

• 22．已知函数f（x）=axe^1-x与g（x）=

  2

  x

  x

  2

  +

  1

  有相同的最大值（其中e为自然对数的底数）．
  （1）求实数a的值；
  （2）证明：∀x∈[0，1]，都有f（x）≥g（x）；
  （3）若直线y=m（m∈R）与曲线y=f（x）有两个不同的交点A（x₁，y₁），B（x₂，y₂），求证：x₁+x₂＜

  2

  m

  ．
  组卷：78引用：3难度：0.3

  解析