当前位置：试卷中心 > 试卷详情

2022-2023学年广东省深圳外国语学校高三（上）第一次月考数学试卷

发布：2024/7/16 8:0:9

一、单选题（本题共8小题，每小题5分，共40分．每小题给出的四个选项中，只有一个选项是符合题目要求的）

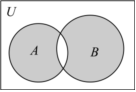1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（　　）

A．（-2，0] B．[-2，0] C．[-2，0]∪{4} D．（-2，0]∪{4}
组卷：454引用：6难度：0.8
解析
2．若复数z所对应的点在第四象限，且满足z²-2z+2=0，则z²=（　　）
A．1+i B．1-i C．-2i D．2i
组卷：79引用：6难度：0.8
解析
3．已知
a
•
b
=
-
24
，
a
+
2
b
=
（
-
5
，
2
）
，若
a
与
b
模相等，则
|
a
|
=（　　）
A．3 B．4 C．5 D．6
组卷：308引用：4难度：0.7
解析
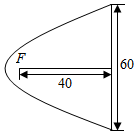4．探照灯反射镜的纵断面是抛物线的一部分，光源放在焦点F处．已知灯口直径为60cm,光源距灯口的深度为40cm,则光源到反射镜的顶点的距离为（　　）
A．5cm B．10cm C．15cm D．20cm
组卷：47引用：2难度：0.8
解析
5．设函数f（x）=（a-1）x|x-b+1|为奇函数且在R上为减函数，则关于a、b的值表述正确的是（　　）
A．a＞1，b=1 B．a＞1，b＜1 C．a＜1，b=1 D．a＜1，b＞1
组卷：80引用：2难度：0.8
解析
6．定义函数迭代：
f^（0）（x）=x
f^（1）（x）=f（x）
f^（2）（x）=f（f（x））
⋯
f^（n+1）（x）=f（f^（n）（x））
已知f（x）=3x+2，则f^（n）（x）=（　　）
A．3ⁿx+3ⁿ-1 B．3ⁿx+3ⁿ+1 C．3nx+3n-1 D．3ⁿx-3ⁿ+1
组卷：51引用：3难度：0.6
解析
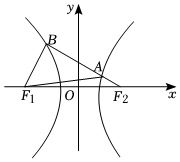7．如图，F₁、F₂是双曲线C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦点，过F₂的直线与双曲线C交于A、B两点．若A是BF₂中点且BF₁⊥BF₂，则该双曲线的渐近线方程为（　　）
A．y=±2
3
x B．y=±2
2
x C．y=±
3
x D．y=±
2
x
组卷：574引用：7难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，共70分，其中17题10分，其余各题12分.解答应写出文字说明、证明过程或演算步骤）

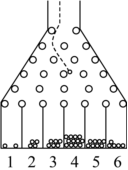21．高尔顿板又称豆机、梅花机等，是英国生物统计学家高尔顿设计用来研究随机现象的模型．如图所示的高尔顿板为一块木板自上而下钉着6层圆柱形小木块，最顶层有2个小木块，以下各层小木块的个数依次递增，各层小木块互相平行但相互错开，小木块之间留有适当的空隙作为通道，前面挡有一块透明玻璃．让小球从高尔顿板上方的通道口落下，小球在下落过程中与层层小木块碰撞，且等可能向左或者向右滚下，最后落入高尔顿板下方从左至右编号为1，2，…，6的球槽内．
（1）某商店将该高尔顿板改良成游戏机，针对某商品推出促销活动．凡是入店购买该商品一件，就可以获得一次游戏机会．若小球落入X号球槽，该商品可立减Y元，其中Y=|20-5X|．若该商品的成本价是10元，从期望的角度考虑，为保证该商品总体能盈利，求该商品的最低定价．（结果取整数）
（2）将79个小球依次从高尔顿板上方的通道口落下，试问3号球槽中落入多少个小球的概率最大？
附：设随机变量ξ～B（n,p），则ξ的分布列为
P
（
ξ
=
k
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
，k=0，1，2，⋯，n.
P
（
ξ
=
k
）
P
（
ξ
=
k
-
1
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
C
k
-
1
n
p
k
-
1
（
1
-
p
）
n
-
k
+
1
=
1
+
（
n
+
1
）
p
-
k
k
（
1
-
p
）
．
组卷：136引用：5难度：0.5
解析
22．设函数f（x）=-xlnx+ax²+x（a∈R）．
（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；
（2）若a=1，k∈N，g（x）=x²+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．
组卷：65引用：4难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2022-2023学年广东省深圳外国语学校高三（上）第一次月考数学试卷

一、单选题（本题共8小题，每小题5分，共40分．每小题给出的四个选项中，只有一个选项是符合题目要求的）

1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（ ）​

2．若复数z所对应的点在第四象限，且满足z2-2z+2=0，则z2=（ ）

3．已知a•b=-24，a+2b=（-5，2），若a与b模相等，则|a|=（ ）

4．探照灯反射镜的纵断面是抛物线的一部分，光源放在焦点F处．已知灯口直径为60cm,光源距灯口的深度为40cm,则光源到反射镜的顶点的距离为（ ）

5．设函数f（x）=（a-1）x|x-b+1|为奇函数且在R上为减函数，则关于a、b的值表述正确的是（ ）

6．定义函数迭代：f（0）（x）=xf（1）（x）=f（x）f（2）（x）=f（f（x））⋯f（n+1）（x）=f（f（n）（x））已知f（x）=3x+2，则f（n）（x）=（ ）

7．如图，F1、F2是双曲线C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦点，过F2的直线与双曲线C交于A、B两点．若A是BF2中点且BF1⊥BF2，则该双曲线的渐近线方程为（ ）

四、解答题（本题共6小题，共70分，其中17题10分，其余各题12分.解答应写出文字说明、证明过程或演算步骤）

22．设函数f（x）=-xlnx+ax2+x（a∈R）．（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；（2）若a=1，k∈N，g（x）=x2+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．

1．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（　　）

2．若复数z所对应的点在第四象限，且满足z²-2z+2=0，则z²=（　　）

3．已知
a
•
b
=
-
24
，
a
+
2
b
=
（
-
5
，
2
）
，若
a
与
b
模相等，则
|
a
|
=（　　）

4．探照灯反射镜的纵断面是抛物线的一部分，光源放在焦点F处．已知灯口直径为60cm,光源距灯口的深度为40cm,则光源到反射镜的顶点的距离为（　　）

5．设函数f（x）=（a-1）x|x-b+1|为奇函数且在R上为减函数，则关于a、b的值表述正确的是（　　）

6．定义函数迭代：
f^（0）（x）=x
f^（1）（x）=f（x）
f^（2）（x）=f（f（x））
⋯
f^（n+1）（x）=f（f^（n）（x））
已知f（x）=3x+2，则f^（n）（x）=（　　）

7．如图，F₁、F₂是双曲线C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦点，过F₂的直线与双曲线C交于A、B两点．若A是BF₂中点且BF₁⊥BF₂，则该双曲线的渐近线方程为（　　）

22．设函数f（x）=-xlnx+ax²+x（a∈R）．
（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；
（2）若a=1，k∈N，g（x）=x²+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．