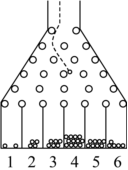
高尔顿板又称豆机、梅花机等，是英国生物统计学家高尔顿设计用来研究随机现象的模型．如图所示的高尔顿板为一块木板自上而下钉着6层圆柱形小木块，最顶层有2个小木块，以下各层小木块的个数依次递增，各层小木块互相平行但相互错开，小木块之间留有适当的空隙作为通道，前面挡有一块透明玻璃．让小球从高尔顿板上方的通道口落下，小球在下落过程中与层层小木块碰撞，且等可能向左或者向右滚下，最后落入高尔顿板下方从左至右编号为1，2，…，6的球槽内．
（1）某商店将该高尔顿板改良成游戏机，针对某商品推出促销活动．凡是入店购买该商品一件，就可以获得一次游戏机会．若小球落入X号球槽，该商品可立减Y元，其中Y=|20-5X|．若该商品的成本价是10元，从期望的角度考虑，为保证该商品总体能盈利，求该商品的最低定价．（结果取整数）
（2）将79个小球依次从高尔顿板上方的通道口落下，试问3号球槽中落入多少个小球的概率最大？
附：设随机变量ξ～B（n,p），则ξ的分布列为
P
（
ξ
=
k
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
，k=0，1，2，⋯，n.
P
（
ξ
=
k
）
P
（
ξ
=
k
-
1
）
=
C
k
n
p
k
（
1
-
p
）
n
-
k
C
k
-
1
n
p
k
-
1
（
1
-
p
）
n
-
k
+
1
=
1
+
（
n
+
1
）
p
-
k
k
（
1
-
p
）
．

【答案】（1）15元；
（2）3号球槽中落入24或25个小球的概率最大．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/16 8:0:9组卷：136引用：5难度：0.5

相似题

1．已知某高校共有10000名学生，其图书馆阅览室共有994个座位，假设学生是否去自习是相互独立的，且每个学生在每天的晚自习时间去阅览室自习的概率均为0.1．
（1）将每天的晚自习时间去阅览室自习的学生人数记为X，求X的期望和方差；
（2）18世纪30年代，数学家棣莫弗发现，如果随机变量X服从二项分布B（n,p），那么当n比较大时，可视为X服从正态分布N（μ，σ²）．任意正态分布都可变换为标准正态分布（μ=0且σ=1的正态分布），如果随机变量Y～N（μ，σ²），那么令Z=
Y
-
μ
σ
，则可以证明Z～N（0，1）．当Z～N（0，1）时，对于任意实数a,记Φ（a）=P（Z＜a）．
已知如表为标准正态分布表（节选），该表用于查询标准正态分布对应的概率值．例如当a=0.16时，由于0.16=0.1+0.06，则先在表的最左列找到数字0.1（位于第三行），然后在表的最上行找到数字0.06（位于第八列），则表中位于第三行第八列的数字0.5636便是Φ（0.16）的值．
（ⅰ）求在晚自习时间阅览室座位不够用的概率；
（ⅱ）若要使在晚自习时间阅览室座位够用的概率高于0.7，则至少需要添加多少个座位？

a 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

0.0 0.500 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359

0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753

0.2 0.5793 0.5834 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141

0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6404 0.6443 0.6480 0.6517

0.4 0.6554 0.6591 0.628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879

0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224

发布：2024/6/27 10:35:59组卷：439引用：4难度：0.4