2022-2023学年天津开发区一中高二（下）期中数学试卷

一、单选题。（本大题共12小题，共36.0分）

• 1．设双曲线C以椭圆

  x

  2

  25

  +

  y

  2

  9

  =

  1

  长轴的两个端点为焦点，以椭圆的焦点为顶点，则双曲线C的方程为（　　）

  A． x 2 25 - y 2 9 = 1

  B． x 2 16 - y 2 4 = 1

  C． x 2 16 - y 2 9 = 1

  D． x 2 9 - y 2 16 = 1
  组卷：92引用：8难度：0.7

  解析

• 2．下列对函数求导运算正确的是（　　）

  A．（sin π 3 ）′=cos π 3

  B．（e2x）′=e2x

  C．（ cosx x ）′= xsinx - cosx x 2

  D．（2ex）′=2ex
  组卷：166引用：4难度：0.7

  解析

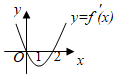• 3．设f′（x）是函数f（x）的导函数，y=f′（x）的图象如图所示，则y=f（x）的图象最有可能的是（　　）

  A．

  B．

  C．

  D．
  组卷：2233引用：195难度：0.9

  解析

• 4．已知直线l₁：mx-3y+6=0，l₂：4x-3my+12=0，若l₁∥l₂，则l₁，l₂之间的距离为（　　）

  A． 12 13 13

  B． 8 13 13

  C． 9 13 13

  D． 13
  组卷：231引用：3难度：0.8

  解析

• 5．已知等差数列{a_n}的公差为2，若a₁，a₃，a₄成等比数列，S_n是{a_n}的前n项和，则S₉等于（　　）

  A．-8

  B．-6

  C．10

  D．0
  组卷：838引用：23难度：0.9

  解析

• 6．已知二项式（2x²-

  1

  x

  ）ⁿ的所有二项式系数之和等于128，那么其展开式中含

  1

  x

  项的系数是（　　）

  A．-84

  B．-14

  C．14

  D．84
  组卷：452引用：21难度：0.7

  解析

• 7．已知等比数列{a_n}中，a₄=2，则a₁a₂…a₇=（　　）

  A．8

  B．14

  C．128

  D．256
  组卷：417引用：6难度：0.8

  解析

三、解答题。（本大题共4小题，共40.0分。解答应写出文字说明，证明过程或演算步骤）

• 20．已知椭圆C：

  x

  2

  b

  2

  +

  y

  2

  a

  2

  =1（a＞b＞0）的离心率为

  3

  2

  ，椭圆C的长轴长为4．
  （1）求椭圆C的方程；
  （2）已知直线l：y=kx+

  3

  与椭圆C交于A，B两点，是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由．
  组卷：130引用：11难度：0.3

  解析

• 21．已知函数f（x）=x²-2alnx,其中（a∈R），
  （1）当函数f（x）在（1，（1））处切线斜率为0时，求函数f（x）在[

  1

  e

  ，e]上的最值；
  （2）讨论函数f（x）的单调性；
  （3）若函数f（x）有两个零点，求a的取值范围．
  组卷：182引用：1难度：0.6

  解析