当前位置：试卷中心 > 试卷详情

2023-2024学年福建省莆田一中高三（上）期初数学试卷

发布：2024/8/13 18:0:1

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

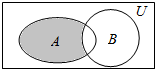1．设全集U=R，集合A={1，2，3，4，5}，B={x∈R|x＞2}，则图中阴影部分所表示的集合为（　　）
A．{0，1} B．{1} C．{1，2} D．{0，1，2}
组卷：84引用：3难度：0.8
解析
2．已知p：x²-x＜0，那么命题p的一个必要不充分条件是（　　）
A．0＜x＜1 B．-1＜x＜1 C．
1
2
＜x＜
2
3
D．
1
2
＜x＜2
组卷：483引用：46难度：0.9
解析
3．若方程mx²+（2m-3）x+m=0（m＞0）有两个不相等的正实数解，则实数m的取值范围是（　　）
A．
（
3
2
，
+
∞
）
B．
（
0
，
3
2
）
C．
（
0
，
3
4
）
D．
（
3
4
，
+
∞
）
组卷：94引用：2难度：0.7
解析
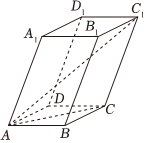4．如图，平行六面体ABCD-A₁B₁C₁D₁的底面ABCD是矩形，
AB
=
2
，
AD
=
2
，AA₁=3，且∠A₁AD=∠A₁AB=45°，则线段AC₁的长为（　　）
A．
2
6
B．5 C．
26
D．
3
3
组卷：36引用：3难度：0.6
解析
5．已知函数f（x）=
（
a
-
1
）
x
+
2
a
,
x
＜
0
x
2
-
2
x
,
x
≥
0
有最小值，则a的取值范围是（　　）
A．[-
1
2
，1） B．（-
1
2
，1） C．[-
1
2
，1] D．（-
1
2
，1]
组卷：206引用：6难度：0.7
解析
6．设f（x）是定义在R上的偶函数，若∀x₁，x₂∈（0，+∞）（x₁≠x₂），都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＜
0
，则（　　）
A．
f
（
lo
g
3
0
.
3
）
＞
f
（
2
-
0
.
3
）
＞
f
（
2
-
0
.
4
）
B．
f
（
lo
g
3
0
.
3
）
＞
f
（
2
-
0
.
4
）
＞
f
（
2
-
0
.
3
）
C．f（2^-0.3）＞f（2^-0.4）＞f（log₃0.3）
D．f（2^-0.4）＞f（2^-0.3）＞f（log₃0.3）
组卷：8引用：2难度：0.7
解析
7．连续抛掷两次骰子，“第一次抛掷结果向上的点数小于3”记为A事件，“第二次抛掷结果向上的点数是3的倍数”记为B事件，“两次抛掷结果向上的点数之和为偶数”记为C事件，“两次抛掷结果向上的点数之和为奇数”记为D事件，则下列叙述中不正确的是（　　）
A．C与D互斥 B．
P
（
D
|
A
）
=
1
2
C．A与C相互独立 D．B与D不相互独立
组卷：32引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70.0分.解答应写出文字说明，证明过程或演算步骤）

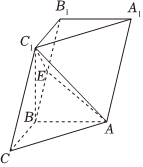21．如图，在三棱柱ABC-A₁B₁C₁中，已知AB⊥侧面BB₁C₁C，
BC
=
2
，AB=CC₁=2，
∠
BC
C
1
=
π
4
，点E在棱BB₁上．
（1）证明：C₁B⊥平面ABC；
（2）若BE=λBB₁，试确定λ的值，使得C到平面AC₁E的距离为
4
5
5
．
组卷：44引用：4难度：0.6
解析
22．已知某次比赛的乒乓球团体赛采用五场三胜制，第一场为双打，后面的四场为单打．团体赛在比赛之前抽签确定主客队．主队三名选手的一单、二单、三单分别为选手A、B、C，客队三名选手的一单、二单、三单分别为选手X、Y、Z．比赛规则如下：第一场为双打（YZ对阵BC）、第二场为单打（X对阵A）、第三场为单打（Z对阵C）、第四场为单打（Y对阵A）、第五场为单打（X对阵B）．已知双打比赛中YZ获胜的概率是
1
4
，单打比赛中X、Y、Z分别对阵A、B、C时，X、Y、Z获胜的概率如表：

选手
选手 A B C

X
2
3

1
2

1
3

Y
1
3

1
2

2
3

Z
1
4

2
3

1
2

（1）求主、客队分出胜负时恰进行了3场比赛的概率；
（2）客队输掉双打比赛后，能否通过临时调整选手Y为三单、选手Z为二单使得客队团体赛获胜的概率增大？请说明理由．
组卷：108引用：7难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．C与D互斥	B． P （ D \| A ） = 1 2
C．A与C相互独立	D．B与D不相互独立

选手选手	A	B	C
X	2 3	1 2	1 3
Y	1 3	1 2	2 3
Z	1 4	2 3	1 2

2023-2024学年福建省莆田一中高三（上）期初数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．设全集U=R，集合A={1，2，3，4，5}，B={x∈R|x＞2}，则图中阴影部分所表示的集合为（ ）

2．已知p：x2-x＜0，那么命题p的一个必要不充分条件是（ ）

3．若方程mx2+（2m-3）x+m=0（m＞0）有两个不相等的正实数解，则实数m的取值范围是（ ）

4．如图，平行六面体ABCD-A1B1C1D1的底面ABCD是矩形，AB=2，AD=2，AA1=3，且∠A1AD=∠A1AB=45°，则线段AC1的长为（ ）

5．已知函数f（x）=（a-1）x+2a,x＜0x2-2x,x≥0有最小值，则a的取值范围是（ ）

6．设f（x）是定义在R上的偶函数，若∀x1，x2∈（0，+∞）（x1≠x2），都有f（x1）-f（x2）x1-x2＜0，则（ ）

四、解答题（本大题共6小题，共70.0分.解答应写出文字说明，证明过程或演算步骤）

21．如图，在三棱柱ABC-A1B1C1中，已知AB⊥侧面BB1C1C，BC=2，AB=CC1=2，∠BCC1=π4，点E在棱BB1上．（1）证明：C1B⊥平面ABC；（2）若BE=λBB1，试确定λ的值，使得C到平面AC1E的距离为455．

1．设全集U=R，集合A={1，2，3，4，5}，B={x∈R|x＞2}，则图中阴影部分所表示的集合为（　　）

2．已知p：x²-x＜0，那么命题p的一个必要不充分条件是（　　）

3．若方程mx²+（2m-3）x+m=0（m＞0）有两个不相等的正实数解，则实数m的取值范围是（　　）

4．如图，平行六面体ABCD-A₁B₁C₁D₁的底面ABCD是矩形，
AB
=
2
，
AD
=
2
，AA₁=3，且∠A₁AD=∠A₁AB=45°，则线段AC₁的长为（　　）

5．已知函数f（x）=
（
a
-
1
）
x
+
2
a
,
x
＜
0
x
2
-
2
x
,
x
≥
0
有最小值，则a的取值范围是（　　）

6．设f（x）是定义在R上的偶函数，若∀x₁，x₂∈（0，+∞）（x₁≠x₂），都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＜
0
，则（　　）

21．如图，在三棱柱ABC-A₁B₁C₁中，已知AB⊥侧面BB₁C₁C，
BC
=
2
，AB=CC₁=2，
∠
BC
C
1
=
π
4
，点E在棱BB₁上．
（1）证明：C₁B⊥平面ABC；
（2）若BE=λBB₁，试确定λ的值，使得C到平面AC₁E的距离为
4
5
5
．