2022-2023学年福建省莆田二中高二(上)第二次月考数学试卷
发布:2024/7/31 8:0:9
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求的.
-
1.两直线3x+4y-3=0与mx+8y+1=0平行,则它们之间的距离为( )
组卷:249引用:6难度:0.7 -
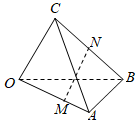 2.如图,空间四边形OABC中,,OA=a,OB=b,且OC=c,OM=2MA,则BN=NC等于( )MN组卷:277引用:12难度:0.9
2.如图,空间四边形OABC中,,OA=a,OB=b,且OC=c,OM=2MA,则BN=NC等于( )MN组卷:277引用:12难度:0.9 -
3.已知双曲线
的一个焦点为(-2,0),则双曲线C的一条渐近线方程为( )C:x2a2-y2=1组卷:265引用:2难度:0.9 -
 4.一种卫星接收天线如图所示,其曲面与轴截面的交线为抛物线.在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚集到信号装置(信号装置安装在抛物线的焦点处).已知接收天线的口径(直径)为5 m,深度为1 m,则信号装置与卫星接收天线中心O的距离为( )组卷:80引用:3难度:0.9
4.一种卫星接收天线如图所示,其曲面与轴截面的交线为抛物线.在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线,经反射聚集到信号装置(信号装置安装在抛物线的焦点处).已知接收天线的口径(直径)为5 m,深度为1 m,则信号装置与卫星接收天线中心O的距离为( )组卷:80引用:3难度:0.9 -
5.已知数列{an}的通项公式为
.若数列{an}的前n项和为Sn,则Sn取得最大值时n的值为( )an=-2n2+9n(n∈N*)组卷:170引用:4难度:0.7 -
6.动点P,Q分别在抛物线x2=4y和圆x2+y2-8y+13=0上,则|PQ|的最小值为( )
组卷:100引用:2难度:0.6 -
7.已知圆C:(x+1)2+(y-4)2=m(m>0)和两点A(-2,0),B(1,0),若圆C上存在点P,使得|PA|=2|PB|,m的取值范围是( )
组卷:227引用:10难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知F是抛物线C:y2=2px(p>0)的焦点,点M(t,4)在抛物线上,且
.|MF|=54t
(1)求C的方程;
(2)过C上一动点P(x0,y0)(y0≠0)作C的切线l交x轴于点Q.判断线段PQ的中垂线是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.组卷:71引用:2难度:0.5 -
22.已知椭圆
的左、右焦点分别为F1,F2,过右焦点F2作直线l交C于A(x1,y1),B(x2,y2),其中y1>0,y2<0,△ABF1的周长为C:x2a2+y2b2=1(a>b>0),C的离心率为42.22
(1)求C的方程;
(2)已知△AF1F2的重心为G,设△BF1G和△ABF1的面积比为λ,求实数λ的取值范围.组卷:64引用:2难度:0.4


