2023年山东省烟台市开发区中考数学一模试卷

一、选择题（本题共10个小题，每小题3分，满分30分）每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的。

• 1．|-2|的倒数是（　　）

  A．2

  B．-2

  C． 1 2

  D． - 1 2
  组卷：578引用：82难度：0.9

  解析

• 2．下列图形是四届数学大会会标，其中不属于中心对称的有（　　）
  

  A．1个

  B．2个

  C．3个

  D．4个
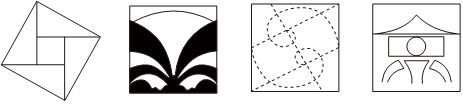  组卷：22引用：2难度：0.7

  解析

• 3．计算a²•a³的结果是（　　）

  A．a2

  B．a3

  C．a5

  D．a6
  组卷：1426引用：24难度：0.9

  解析

• 4．如图所示，该几何体的左视图是（　　）
  

  A．

  B．

  C．

  D．
  组卷：193引用：5难度：0.7

  解析

• 5．一个正多边形的内角和是1260°，则这个正多边形的一个外角等于（　　）

  A．60°

  B．45°

  C．72°

  D．40°
  组卷：725引用：5难度：0.7

  解析

• 6．第24届冬奥会期间，小明收集到4张卡片，正面图案如图所示，它们除此之外完全相同，把这4张卡片背面朝上洗匀后摸出1张，放回洗匀再摸出一张，则这两张卡片正面图案恰好是两张滑雪的概率是（　　）

  A． 1 6

  B． 1 8

  C． 1 12

  D． 1 4
  组卷：41引用：1难度：0.6

  解析

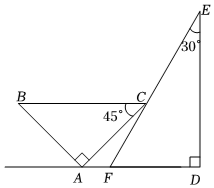• 7．将两块三角板按如图所示位置摆放，若AD∥BC，点F在AD上，则∠ACF的度数为（　　）

  A．15°

  B．10°

  C．20°

  D．25°
  组卷：227引用：6难度：0.7

  解析

• 8．将一个长为2a,宽为2b的矩形纸片（a＞b），用剪刀沿图1中的虚线剪开，分成四块形状和大小都一样的小矩形纸片，然后按图2的方式拼成一个正方形，则中间小正方形的面积为（　　）
  

  A．a2+b2

  B．a2-b2

  C．（a+b）2

  D．（a-b）2
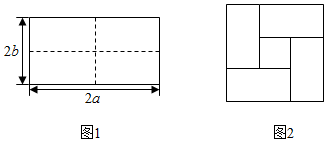  组卷：1471引用：13难度：0.8

  解析

三、解答题（本大题共8个小题，满分72分）

• 23．问题情境：
  如图1，点E为正方形ABCD内一点，∠AEB=90°，将Rt△ABE绕点B按顺时针方向旋转，得到△CBE′（点A的对应点为点C），延长AE交CE′于点F，连接DE．
  猜想证明：
  （1）试判断四边形BE′FE的形状，并说明理由；
  （2）如图2，若DA=DE，请猜想线段CF与FE′的数量关系并加以证明；
  解决问题：
  （3）如图1，若AB=15，CF=3，请直接写出EF和DE的长．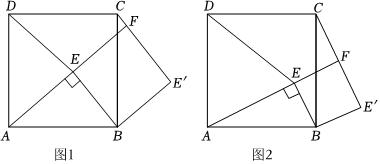
  ​
  组卷：161引用：1难度：0.1

  解析

• 24．抛物线y=ax²+bx-6与x轴交于A（3，0），B（8，0）两点，与y轴交于点C，点P在抛物线上，设点P的横坐标为m.
  （1）求a,b的值以及直线BC的表达式；
  （2）如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标：
  （3）如图2，若点P在直线BC上方的抛物线上，PN∥y轴交BC于点N，PQ⊥BC，垂足为点Q，线段PQ是否有最大值？如果有，请求出最大值及此时点P的坐标；如果没有，请说明理由．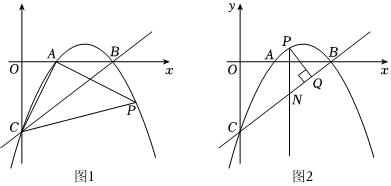
  
  组卷：141引用：1难度：0.3

  解析